Bài giảng môn học Hình học lớp 7 - Xoay quanh một bài toán hình học
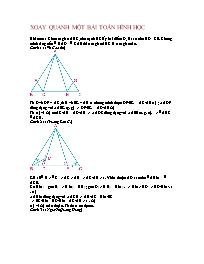
Bài toán : Cho tam giác ABC, trên cạnh BC lấy hai điểm D, E sao cho BD = CE. Chứng minh rằng nếu Đ BAD = Đ CAE thì tam giác ABC là tam giác cân.
Cách 1 : (Vũ Cao Ân)
Bạn đang xem 20 trang mẫu của tài liệu "Bài giảng môn học Hình học lớp 7 - Xoay quanh một bài toán hình học", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
XOAY QUANH MỘT BÀI TOÁN HÌNH HỌC Bài toán : Cho tam giác ABC, trên cạnh BC lấy hai điểm D, E sao cho BD = CE. Chứng minh rằng nếu Đ BAD = Đ CAE thì tam giác ABC là tam giác cân. Cách 1 : (Vũ Cao Ân) Từ D vẽ DF // AC, từ E vẽ EG // AB ta chứng minh được DF/EG = AC/AB (1) ; ΔADF đồng dạng với ΔAEG (g. g) => DF/EG = AD/AE (2) Từ (1) và (2) có AC/AB = AD/AE => ΔADC đồng dạng với ΔAEB (c. g. c). => Đ ABC = Đ ACB. Cách 2 : (Trương Sơn Ca) Giả sử Đ B > Đ C => AC > AB => AC/AB > 1. Vẽ M thuộc AD sao cho Đ ABM = Đ ACE. Có Đ M1 = góc E1 => Đ M2 = Đ E2 ; góc D1 > Đ E2 = Đ M2 . => BM > BD => BD/BM < 1 . (1) ΔABM đồng dạng với ΔACE => AB/AC = BM/EC => EC/BM = BD/BM = AC/AB > 1 . (2) (1) và (2) mâu thuẫn. Từ đó ta có đpcm. Cách 3 : (Nguyễn Quang Hùng) Từ D và E lần lượt vẽ DF vuông góc với AB ; EG vuông góc với AC. BD = CE => SABD = SACE => AB.DF = AC.EG => DF/EG = AC/AB (1). ΔADF đồng dạng với ΔAEG => DF/EG = AD/AE (2) Từ (1) và (2) => AC/AB = AD/AE , cho ta ΔABE đồng dạng với ΔACD => Đ ABE = Đ ACD. Cách 4 : (Minh Quân) Vẽ hình bình hành ABEF => BE = AF. Chứng minh được tứ giác ADCF là hình bình hành => Đ EFC = Đ BAD = Đ EAC (gt). ΔAEG đồng dạng với ΔFCG (g. g) => AG/FG = EG/CG (1) Do AG/GC = FG/GE (AF // EC) => AG/FG = EG/CG (2) Từ (1) và (2) có EG = GC cân tại G => ΔGEC cân tại G => Đ FEC = Đ ACE => Đ ABC = Đ ACB. Cách 5 : (Đỗ Đăng Trí) Vẽ BH, CK là các đường cao của các tam giác ABD, ACE. BD = CE => SABD = SACE => BH/CK = AE/AD ΔABH đồng dạng với ΔACK => BH/CK = AB/AC ΔABE đồng dạng với ΔACD ( Đ BAE = Đ CAD , AB/AC = AE/AD) => Đ ABE = Đ ACD => Δ ABC cân tại A. Cách 6 : (Bảo Linh) Qua B vẽ đường thẳng song song AC cắt AD tại M, qua C vẽ đường thẳng song song AB cắt AE tại N. ΔABM đồng dạng với ΔACN (g. g) => AB/AC = BM/CN (1) ΔADC có BM // AC => AC/BM = BE/BD ΔABE có CN // AB => AB/CN = BE/EC Do đó có AB/AC = CN/BM (2) Từ (1) và (2) có AB/AC.AB/AC = BM/CN.CN/BM => AB2/AC2 = 1 => AB = AC. PHƯƠNG PHÁP CHỨNG MINH BA ĐIỂM ĐỒNG QUY Các bạn đã học qua lớp 7 chắc chắn đều biết về các đường đồng quy của tam giác : Định lí 1 : Ba đường trung tuyến của một tam giác cùng đi qua một điểm ; Định lí 2 : Ba đường phân giác của một tam giác cùng đi qua một điểm ; Định lí 3 : Ba đường trung trực của một tam giác cùng đi qua một điểm ; Định lí 4 : Ba đường cao của một tam giác cùng đi qua một điểm. SGK Toán 7 tập 2 đã sử dụng cùng một phương pháp chứng minh ba đường thẳng đồng quy để chứng minh định lí 2, định lí 3. Phương pháp chứng minh này có thể mô tả khái quát như sau : Ba đường thẳng a, b, c đồng quy nếu : - Mọi điểm thuộc c đều có tính chất C và ngược lại. - Chứng tỏ giao điểm của a và b thỏa mãn tính chất C. Các bạn cần lưu ý, quỹ tích các điểm thỏa mãn tính chất C chính là đường thẳng c. Như vậy mấu chốt của phương pháp này chính là việc phát hiện ra tính chất C. Nếu ta phát hiện ra nhiều tính chất của đường thẳng c thì cũng có nghĩa là sẽ có nhiều cách chứng minh a, b, c đồng quy. Ta sẽ áp dụng phương pháp này để chứng minh các định lí trên. * Chứng minh định lí 1 : Cách 1 : - Bổ đề 1 : Trong một tam giác, quỹ tích trung điểm các đoạn thẳng nối hai điểm lần lượt nằm trên hai cạnh khác nhau, song song với cạnh thứ ba là trung tuyến thuộc cạnh thứ ba đó. - Gọi AM, BN, CK lần lượt là các trung tuyến của ∆ABC ; G = BN ∩ CK. Qua G dựng DE // BC, FR // AB, PQ // AC (hình 1). Theo bổ đề 1 ta có GF = GR ; GP = GQ. Từ đó dễ thấy ∆DQG = ∆FGP ; ∆FGP = ∆GRE (g.c.g) => ∆DQG = ∆GRE => DG = GE=> G Є AM (theo bổ đề 1). Vậy AM, BN, CK đồng quy tại G. Định lí 1 được chứng minh. Cách 2 : (hướng dẫn) - Bổ đề 2 : Quỹ tích các điểm nằm trong một tam giác với các cạnh a, b, c, có tỉ số khoảng cách tới hai cạnh b, c là c/b là trung tuyến thuộc cạnh a. - Gọi AM, BN, CK lần lượt là các trung tuyến của ∆ABC ; G = BN ∩ CK. Dựng GD ^ AB, GE ^ AC, GF ^ BC. Theo bổ đề 2 suy ra : GD/GF = BC/AB ; GF/GE = AC/BC ; => GD/GE = GD/GF . GF/GE = BC/AC . AC/BC = AC/BC ; * Chứng minh định lí 2 : (sử dụng kết quả khác với SGK) - Bổ đề 3 : Trong ∆ABC, DE // BC (D Є AB, E Є AC), quỹ tích điểm I thuộc DE sao cho ID/IE = AB/AC là đường phân giác AA1. - Gọi AA1, BB1, CC1 lần lượt là các phân giác của ∆ABC ; I = BB1 ∩CC1. Qua I dựng DE // BC, FR // AB, PQ // AC (hình 2). Từ bổ đề 3 suy ra : IF/IR = BC/AC ; IQ/IP = AB/BC ; Mặt khác, ta nhận thấy các tam giác IFP, RIE, QDI đôi một đồng dạng => ID/IE = ID/FP . FP/IE = IQ/IP . IF/IR = AB/BC . BC/AC = AB/AC. => ID/IE = AB/AC => I Є AA1 (theo bổ đề 3). Vậy AA1, BB1, CC1 đồng quy tại I. Định lí 2 được chứng minh. * Chứng minh định lí 4 : - Bổ đề 4 : Cho ∆ABC, N thuộc đường cao BB’ và K thuộc đường cao CC’ sao cho DE // BC (D Є AB, E Є AC). Quỹ tích điểm H thuộc DE sao cho HD/DE = BK2/CN2 là đường cao AA’. Hướng dẫn : (hình 3) Hai tam giác vuông ANC và AKB có NB’ ∩ AC ; KC’ ∩ AB => AN2 = AB’.AC ; AK2 = AC’.AB (1). Hai tam giác vuông AB’B và AC’C đồng dạng vì có chung Ð BAC => AB’.AC = AC’.AB (2). Từ (1) và (2) => AN = AK. Gọi M Є AA’ sao cho Ð BMC = 90o tương tự ta có : AN = AK ; BM = BK ; CM = CN (3). Xét tam giác vuông BMC, MA’ ^ BC => BM2 = BA’.BC và CM2 = CA’.BC => BA'/CA' = BM2/CM2 = BK2/CN2 = HD/HE (theo bổ đề 3) => nếu H’ = DE ∩ AA’ thì H'D/H'E = BA'/CA' = HD/HE => H’ ≡ H. Trở lại định lí 4 (hình 4) - Gọi M, N, K lần lượt nằm trên các đường cao AA’, BB’, CC’ của ∆ABC sao cho Ð BMC = Ð ANC = Ð AKB = 90o, H = BB’ ∩ CC’. Qua H dựng DE // BC, FR // AB, PQ // AC. Từ bổ đề 4 suy ra : HQ/HP = AK2/CM2 ; HF/HR = BN2/AN2 Mặt khác, ta nhận thấy các tam giác HFP, RHE, QDH đôi một đồng dạng nên : HD/HE = HD/FP . FP/HE = HQ/HF . HF/HR = AK2/CM2 . BM2/AN2 => HD/HE = BM2/CM2 (Do AK = AN) => H Є AA’ (theo bổ đề 4). Vậy AA’, BB’, CC’ đồng quy tại H. Định lí 4 được chứng minh. * Đề nghị bạn đọc chứng minh các bổ đề 1 ; 2 ; 3 và làm bài tập sau. Bài tập : Trong một tam giác, đường thẳng đối xứng với đường trung tuyến qua đường phân giác cùng xuất phát từ một đỉnh được gọi là đường đối trung của đỉnh đó. Chứng minh rằng trong tam giác, ba đường đối trung đồng quy. Như vậy thông qua hai chứng minh định lí của SGK, ta đã rút ra được một phương pháp chứng minh ba đường thẳng đồng quy rất hiệu quả. Tôi hi vọng các bạn sẽ thành công trong nhiều trường hợp khác. TẬP "LỘI NGƯỢC" ... KHI GIẢI TOÁN “Lội ngược dòng” là một cụm từ quen thuộc trong thể thao, dùng để chỉ những cố gắng đảo ngược kết quả của một trận đấu. Còn “lội ngược dòng” khi giải toán là quá trình phân tích đi lên từ kết quả để tìm ra lời giải. Với mỗi hướng “lội ngược dòng” ta sẽ có thể tìm ra một cách giải. Ta xét bài toán sau : Bài toán : (định lí Py-ta-go) Cho ∆ABC vuông tại A, BC = a, AC = b, AB = c. Chứng ming rằng : a2 = b2 + c2 (*) Hướng 1 : Từ a2, b2, c2 ta liên hệ đến diện tích của các hình vuông có cạnh là a, b, c. Nếu dựng về phía ngoài của ∆ABC các hình vuông có cạnh lần lượt là BC, CA, AB thì (*) tương đương với diện tích hình vuông cạnh BC bằng tổng diện tích của hai hình vuông có cạnh CA, AB. Ta tiếp tục đặt vấn đề : liệu có thể chia hình vuông cạnh BC thành hai hình chữ nhật có diện tích bằng diện tích của hai hình vuông còn lại không. Từ đó ta phát hiện ra đường HH’, trong đó H là chân đường vuông góc hạ từ A của ⇼ABC. Cách 1 : Dựng về phía ngoài của ∆ABC các hình vuông AEFB, BMNC, CPQA (hình 1). Đường cao AH ^ BC cắt MN tại H’ (H Є BC). Đặt BH = c’ và CH = b’. Ta cần chứng minh : SCNH’H = SCPQA ; SBMH’H = SAEFB hay a.b’ = b2 ; a.c’ = c2 (**). Thật vậy, vì hai tam giác vuông ABC và HBA có chung nên ∆ABC đồng dạng với ∆HBA suy ra : AB/HB = BC/AB => AB2 = HB.BC => c2 = a.c'. Tương tự ta có b2 = ab’. Định lí được chứng minh và nếu biết trước (**) thì ta cũng không cần vẽ thêm các hình vuông phụ. Hướng 2 : Ta có : a2 = b2 + c2 = (b + c)2 - 2bc a2 + 4. 1/2 bc = (b + c)2 : (1). Liên hệ với các công thức tính diện tích, ta nhận thấy a2 và (b + c)2 là diện tích các hình vuông có cạnh a và b + c ; 1/2 bc là diện tích tam giác có hai cạnh bên là b và c. Từ đây ta thử tìm cách dựng hình phụ và chứng minh. Cách 2 : Dựng hình vuông ADEF có độ dài cạnh là b + c ; B Є AD ; C Є AF (hình 2). Lấy I Є EF ; K Є DE sao cho IF = KE = b. Ta nhận thấy ∆ABC = ∆DKB = ∆EIK = ∆FCI ; BCIK là hình vuông. => SBCIK + SABC + SDKB + SEIK + SFCI = SADEF SBCIK + 4.SABC = SADEF a2 + 4. 1/2 bc = (b + c)2 a2 = b2 + c2. Hướng 3 : Thay đổi cách nhìn một chút so với cách 2, ta thấy : (*) 1/2(b + c)(b + c) = 1/2a2 + 2. 1/2bc , trong đó vế trái là diện tích của hình thang có hai đáy là b, c và có đường cao là b + c. Cách 3 : Trên tia đối của tia CA, lấy điểm F sao cho CF = c ; Dựng điểm D thuộc nửa mặt phẳng có bờ AE, chứa điểm B, DE ^ AE, DE = b (hình 3). Ta nhận thấy ABDE là hình thang vuông có hai đáy AB = c, DE = b, đường cao AE = b + c ; ∆ABC = ∆ECD ; ∆BCD vuông cân tại C có cạnh là a. => SABDE = SBCD + SABC + SECD SABDE = SBCD + 2.SABC 1/2(b + c)(b + c) = 1/2a2 + 2. 1/2bc a2 = b2 + c2. Hướng 4 : Tiếp tục biến đổi (*) theo hướng khác, a2 = b2 + c2 = (b - c)2 + 2bc a2 = (b - c)2 + 4. 1/2bc. Cách 4 : Không mất tính tổng quát, giả sử b > c. Dựng hình chữ nhật ABA’C ; hình vuông BCED (chứa A’) ; trên BA’ lấy điểm B’ sao cho BB’ = c ; trên DB’ lấy điểm C’ sao cho DC’ = c ; CA’ ∩ EC’ = D’ (hình 4). Ta chứng minh được những kết quả sau : ∆ABC = ∆A’CB = ∆B’BD = ∆C’DE = ∆D’EC và A’B’C’D’ là hình vuông có cạnh là b - c. => SBCED = SA’B’C’D’ + SA’BC + SB’BD + SC’DE + SD’EC SBCED = SA’B’C’D’ + 4.SABC SBCDE = SA'B'C'D' + 4.SABC a2 = (b - c)2 + 4. 1/2bc a2 = b2 + c2. Việc tập “lội ngược dòng” sẽ giúp các bạn tập giải quyết được các bài toán. Các bạn thử tìm lời giải của các bài tập : Bài tập 1 : Cho tứ giác ABCD. Chứng minh rằng : SSABCD ≤ 1/2.AC.BD. Bài tập 2 : Cho a, b, c là ba cạnh của một tam giác và p là nửa chu vi của tam giác đó. Chứng minh rằng : PHƯƠNG TRÌNH CHỨA ẨN TRONG DẤU GIÁ TRỊ TUYỆT ĐỐI Trong chương trình môn Toán THCS, các bạn đã được học và làm quen với phương trình chứa ẩn trong dấu giá trị tuyệt đối. Bài viết giúp các bạn có một số phương pháp cơ bản để xét phương trình loại này. Phương pháp 1 :1 Phương pháp chia khoảng trên trục số. Ta xét dấu các biểu thức trong dấu giá trị tuyệt đối để khử dấu giá trị tuyệt đối. Thí dụ 1 : Giải phương trình : |2x - 1| + |2x - 5| = 4. (1) Lời giải : Lập bảng khử dấu giá trị tuyệt đối : Từ ... t Ax // By và Ð CBy > Ð ACB. Chứng minh rằng : Ð CBy = Ð xAC + Ð ACB. Gợi ý : Kẻ tia Cm // Ax và chứng minh tương tự bài toán “đầu cá”. Bài toán 6 : Cho hình 7, biết Ax // By và Ð CBy > Ð ACB. Chứng minh rằng : Ð CAx + Ð CBy - Ð CAB = 180o. Gợi ý : Kẻ Cm // Ax. * Từ bài toán 1 đến bài toán 6 đều có các bài toán đảo thú vị đang chờ các bạn tiếp tục khám phá. Sau khi học bài “Tổng ba góc trong một tam giác” của chương II, nếu thay đổi giả thiết của bài toán “đầu cá” : Ax không song song với By thì ta có bài toán sau. Bài toán 7 (bài toán “đuôi cá”) : Cho hình 8. Chứng minh rằng : Ð ACB = Ð MAC + Ð MBC + Ð AMB. Gợi ý : Nối MC kéo dài về phía C, sử dụng tính chất góc ngoài của tam giác. Kết hợp các bài toán trên, ta được bài toán “con cá” hoàn chỉnh. Bài toán 8 (bài toán “con cá”) : Cho hình 9. Tính các góc x, y, z. Lời giải bài toán 8 dành cho bạn đọc. Con đường đi đến bài toán “con cá” thật đơn giản nhưng rất lí thú phải không các bạn ? LTS : Xuất phát từ bài 57 trang 104 SGK Toán 7, tập 1), thầy giáo Nguyễn Đức Tấn (TP. HCM) cũng đã tổng quát mối liên hệ giữa ba góc Ð OAa, Ð AOB, Ð OBb (xem hình 3). Từ đó hình thành loạt bài toán tính số đo của một góc biết số đo của hai góc còn lại và các bài toán đảo. MỘT PHƯƠNG PHÁP THÚ VỊ GIẢI BÀI TOÁN TÍNH GÓC Các bài toán về tính số đo góc rất đa dạng, xuất hiện nhiều trong các kì thi. Để giải quyết tốt dạng toán này có khi phải vẽ hình phụ. Trong bài viết này, tôi xin giới thiệu với các em phương pháp vẽ thêm hình phụ là tam giác đều trong bài toán tính số đo góc. Bài toán 1 : Cho tam giác ABC cân tại A, Ð A = 200. Trên AB lấy điểm D sao cho AD = BC. Tính Ð BDC. Lời giải : Cách 1 : Trên nửa mặt phẳng có bờ là đường thẳng BC, chứa điểm A, dựng tam giác đều BCE (hình 1). Vì tam giác ABC cân tại A, Ð A = 200 nên Ð ABC = Ð ACB = 800. Vậy E thuộc miền trong tam giác ABC, suy ra Ð ACE = 200 (1). Dễ thấy ∆ABE = ∆ACE (c.c.c) nên Ð BAE = Ð CAE = Ð A / 2 = 100 (2). Từ (1) suy ra Ð A = Ð ACE = 200 suy ra ∆DAC = ∆ECA (c.g.c), kết hợp với (2) suy ta Ð ACD = Ð CAE = 1010. Ta có Ð BDC là góc ngoài của ∆DAC nên Ð BDC = Ð DAC + Ð DCA = 200 + 100 = 300. Cách 2 : Trên nửa mặt phẳng có bờ là đường thẳng AB, chứa điểm C, dựng tam giác đều ABI (hình 2). Vì ∆ABC cân tại A, Ð A = 200 nên AI = AB = AC ; Ð CAI = 400 ; Ð IBC = 200 suy ra Ð ACI = 700(∆ACI cân tại A) suy ra Ð BCI = 1500 Lại có ∆ADC = ∆BCI (c.g.c) Suy ra Ð ADC = Ð BCI = 1500 suy ra Ð BDC = 300. Bài toán 2 (đề thi vô định toán Nam Tư năm 1983) : Cho tam giác ABC cân tại A, Ð A = 800. Ở miền trong tam giác lấy điểm I sao cho Ð IBC = 100 ; Ð ICB = 300. Tính Ð AIB. Lời giải : Trên nửa mặt phẳng có bờ là đường thẳng BC, chứa điểm A, dựng tam giác đều BCE (hình 3). Vì ∆ABC cân tại A, nên Ð A = 800 nên Ð ABC = Ð ACB = 500 suy ra Ð ABE = Ð ACE = 100 ; điểm A thuộc miền trong tam giác BCE. Dễ dàng chứng minh được ∆AEB = ∆ICB (g.c.g) suy ra BA = BI suy ra ∆ ABI cân tại B, có Ð ABI = 500 - 100 = 400 suy ra Ð AIB = 700. Bài toán 3 : Cho tam giác ABC cân tại A, Ð A = 1000. Trên cạnh AB kéo dài về phía B, lấy điểm E sao cho AE = BC. Tính Ð AEC. Lời giải : Trên nửa mặt phẳng có bờ là đường thẳng AE, chứa điểm C, dựng tam giác đều AEF (hình 4). Vì ∆ABC cân tại A, Ð A = 1000 nên Ð ABC = 400 ; tia AF nằm giữa hai tia AE, AC Suy ra Ð CAF = 400 suy ra ∆ABC = ∆CAF (c.g.c) Suy ra AC = FC suy ra ∆AEC = ∆FEC (c.c.c) Suy ra Ð AEC = Ð FEC = 1 / 2 Ð AEF = 600 / 2 = 300. Qua một số bài toán nêu trên có thể thấy, việc vẽ thêm hình phụ là tam giác đều tỏ ra rất hiệu quả đối với bài toán tính số đo góc bởi vì nó đã tạo ra các góc 60o ; tạo ra nhiều mối quan hệ bằng nhau giữa các cạnh, các góc, các tam giác, ... Các bạn hãy làm thêm bài toán sau : Bài toán 4 : Cho tam giác ABC cân tại A, Ð A = 800. Trên AC lấy điểm E, trên BC lấy điểm F sao cho Ð ABE = Ð CAF = 300. Tính Ð BEF. ĐỊNH LÍ PY - TA - GO MANG ĐẾN NHIỀU BÀI TOÁN THÚ VỊ Khi hỏi một bạn học sinh lớp 8 năm học 2003-2004 : “Nếu một tam giác vuông cân có cạnh góc vuông bằng 1 thì cạnh huyền bằng bao nhiêu ?”, chắc bạn đó sẽ lúng túng. Điều đó cũng dễ hiểu vì trong chương trình môn toán thì năm học 2003-2004 trở về trước, học sinh lớp 8 chưa học căn bậc hai. Nhưng nếu đặt câu hỏi đó cho một học sinh lớp 7 vào cuối học kì I của năm học 2003-2004 thì bạn đó sẽ trả lời : - Quá dễ ! 12 + 12 = 2, đáp số là chứ gì ! Định lí Py-ta-go và căn bậc hai trong sách giáo khoa Toán 7 mới giúp ta có thêm nhiều khả năng tiếp cận những bài toán thú vị. 1. Bài toán tính độ dài đoạn thẳng Ví dụ 1 : Tính các độ dài x, y trên hình 1. Lời giải : áp dụng định lí Py-ta-go vào các tam giác vuông AHC, AHB ta có : x2 = 162 + AH2 ; y2 = 92 + AH2. Do đó : x2 - y2 = (162+ AH2) - (92 + AH2) = 175 (1) Áp dụng định lí Py-ta-go vào tam giác vuông BAC : x2 + y2 = (9 + 16)2 = 625 (2) Từ (1) và (2) suy ra x2 = 400 ; y2 = 225. Do đó : x = 20 ; y = 15. Ví dụ 2 : Một tam giác có độ dài hai cạnh bằng 3 và 8, góc xen giữa bằng 60o. Tính độ dài cạnh còn lại. Lời giải : (hình 2) Xét tam giác ABC có AB = 8 ; AC = 3. Kẻ đường cao AH. Tam giác vuông AHB có ĐA = 60o nên AH = AB : 2 = 8 : 2 = 4. Do AC = 3 nên C nằm giữa A và H và CH = AH - AC = 4 - 3 = 1. Áp dụng định lí Py-ta-go vào các tam giác vuông CHB, AHB ta có : BC2 = BH2 + CH2 = (AB2 - AH2 ) + CH2 = 82 - 42 + 12 = 49. Vậy BC = 7. Ví dụ 3 : Tính chu vi của đường gấp khúc ABCDEA trên hình 3. Hướng dẫn : Hãy kéo dài AB và ED cho cắt nhau tại I.Ááp dụng định lí Py-ta-go vào tam giác vuông AIE, ta tính được AE = 5, do đó chu vi đường gấp khúc ABCDEA bằng 12. 2. Bài toán tính diện tích tam giác Ví dụ 4 : Cho tam giác đều ABC có cạnh bằng 1dm. Số nào trong các số sau cho giá trị sát nhất với diện tích tam giác ABC : 0,4 dm2 ; 0,5 dm2 ; 0,6 dm2 ? Lời giải : (hình 4) Kẻ đường cao AH. Áp dụng định lí Py-ta-go vào tam giác vuông AHC ta có : AH2 = AC2 - HC2 = 12 - 0,52 = 0,75. Giá trị sát nhất với diện tích tam giác ABC là 0,4 dm2. Hướng dẫn : Chú ý rằng 10 = 32 + 12 ; 20 = 22 + 42 ; 50 = (3 + 2)2 + (1 + 4)2. Lời giải : Vẽ thêm các điểm D, H, E như trên hình 5. Ta tính được SADB = 1,5 ; SBHC = 4 ; SBDEH = 2 ; SAEC = 12,5. Do đó : SABC = 12,5 - 1,5 - 4 - 2 = 5. Mời các bạn tự giải các bài tập sau : Bài 1 : Một tam giác vuông cân có cạnh góc vuông bằng 2. Cạnh huyền của tam giác có giá trị sát nhất với số nào trong các số sau : 2,6 ; 2,7 ; 2,8 ; 3. Bài 2 : Một tam giác có độ dài hai cạnh bằng 7 và 5, góc xen giữa bằng 60o. Tính độ dài cạnh thứ ba. Bài 3 : Một tam giác có độ dài hai cạnh bằng 5 và 6, góc xen giữa bằng 120o. Tính độ dài cạnh thứ ba. Bài 4 (bài toán của Xem Lôi-đơ) : ở một hội chợ, người ta quảng cáo bán một cái hồ hình tam giác và ba miếng đất hình vuông dựng trên ba cạnh đó (hình 6). Diện tích ba miếng đất đó bằng 74 acrơ ; 116 acrơ ; 370 acrơ (1acrơ = 4047m2). Bảng quảng cáo không nói rõ diện tích của cái hồ làm nhiều người thắc mắc không rõ diện tích đó lớn hay nhỏ. Bạn hãy tìm diện tích của hồ. Hướng dẫn : 74 = 72 + 52 ; 116 = 102 + 42. Các bạn học sinh lớp 7 thân mến ! Trong TTT2 số 2 và số 16 đã từng đề cập đến việc sử dụng diện tích trong chứng minh hình học cũng như một số bài toán về diện tích. Trong bài viết này tôi xin nêu thêm một số ứng dụng khác của diện tích tam giác vào việc chứng minh một số dạng bài tập. 1. Quan hệ đoạn thẳng Bài toán 1 : Cho tam giác ABC, trung tuyến AM. Một đường thẳng song song với BC cắt các cạnh AB, AC và trung tuyến AM lần lượt tại D, E, F. Chứng minh rằng FD = FE. Lời giải : Hạ DK và EH vuông góc với AM (K, H thuộc AM). Ta có : S(ABM) = S(ACM) (chung đường cao, hai đáy bằng nhau) ; S(DBM) = S(ECM) (đường cao bằng nhau, hai đáy bằng nhau). Suy ra S(DAM) = S(ABM) - S(DBM) = S(ACM) - S(ECM) = S(EAM). Hai tam giác DAM và EAM lại có chung đáy AM nên các đường cao hạ xuống AM bằng nhau hay DK = EH. Từ đó ta có ∆KDF = ∆HEF (g.c.g) suy ra FD = FE. Lời bình : Bài toán không có gì khó khăn nếu ta dùng định lí Ta-lét, tuy nhiên bằng kiến thức về diện tích và kiến thức hình học lớp 7 bài toán đã được chứng minh gọn gàng và đẹp đẽ. Bài toán 2 : Cho tam giác ABC, N là trung điểm của trung tuyến AM. Tia BN cắt cạnh AC tại K. Chứng minh rằng : AK = 1/2 CK, NK = 1/3 NB. Lời giải : Dễ thấy S(ABN) = S(BMN) = S(CMN) = S(CAN) suy ra S(ABN)/S(CBN) = 1/2. Mặt khác các cặp tam giác NAK và NCK ; BAK và BCK đều có chung đường cao tương ứng với hai đáy AK, CK nên Suy ra AK = 1/2 CK Từ đó S(ANK) = 1/2S(CNK) = 1/3 S(NAC) = 1/3 S(ABN) suy ra S(ANK) / S(ABN) = 1/3 => NK = 1/3 BN do hai tam giác có chung đường cao tương ứng với hai đáy NK, BN. Lời bình : Nếu sử dụng kiến thức đường trung bình trong tam giác thì đây là bài toán rất quen thuộc. Đáng tiếc ở lớp 7 chưa được học về đường trung bình. 2. Chứng minh đồng quy, thẳng hàng Bài toán 3 : Cho tam giác ABC, trung tuyến AM. Một đường thẳng song song với BC cắt AB, AC lần lượt tại D và E. Chứng minh rằng BE và CD cắt nhau trên AM. Lời giải : Gọi giao điểm của DE và AM là F, theo bài toán 1 ta có FD = FE, suy ra S(BDFM) = S(BFD) + S(BFM) = S(CFE) + + S(CFM) = S(CEFM) (1). Gọi giao điểm của BE và CD là O, nối OF, OM ta có S(DOF) = S(EOF) (do FD = FE) ; S(BOM) = S(COM) ; S(BDO) = S(CEO) (do S(BDC) = S(BEC)). Suy ra S(BDFOM) = S(CEFOM) hay đường gấp khúc FOM chia đôi diện tích hình thang BDEC (2). Từ (1) và (2) suy ra S(FOM) = 0 ị F, O, M thẳng hàng ị O thuộc FM (đpcm). Lời bình : 1) Đôi khi để chứng minh ba điểm thẳng hàng ta phải chứng minh tam giác có ba đỉnh là ba điểm ấy có diện tích bằng 0. 2) Kết hợp kết quả của bài toán 1 và bài toán 3 ta có bài toán sau : “Trong một hình thang, giao điểm hai cạnh bên kéo dài, giao điểm hai đường chéo và hai trung điểm của hai đáy là bốn điểm thẳng hàng” (Bổ đề hình thang). Bài toán 4 : (tính chất ba đường trung tuyến trong tam giác) Trong một tam giác, ba đường trung tuyến đồng quy và điểm đồng quy chia mỗi trung tuyến theo tỉ số 2/3 kể từ đỉnh. Lời giải : Vẽ các trung tuyến BE và CF cắt nhau tại G. Nối AG cắt BC tại M. Ta sẽ chứng minh MB = MC. Ta có S(ABE) = S(ACF) = 1/2 S(ABC) suy ra S(BGF) = S(CGE) => S(AGF) = S(BGF) = S(CGE) = S(AGE) => S(ABG) = S(ACG) (*). Hạ các đường vuông góc BH, CK tới AM. Do (*) nên BH = CK, suy ra S(GBM) = S(GCM) => BM = CM. Mặt khác, do S(ABG) = 2S(AGE) suy ra BG = 2GE hay BG/BE = 2/3 Tương tự ta có :AG/AM = CG/CF = 2/3 Lời bình : Đây là một tính chất quan trọng của hình học nhưng do hạn chế về kiến thức (chưa học về đường trung bình trong tam giác) nên khi đưa vào chương trình lớp 7 chỉ yêu cầu học sinh thừa nhận. (Kì sau đăng tiếp)
Tài liệu đính kèm:
 chuyen de lop 7 suu tam.doc
chuyen de lop 7 suu tam.doc





