Bài soạn môn Hình học 7 - Tuần 28

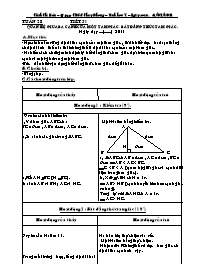
TUầN 28 Tiết 51 
Quan hệ giữa ba cạnh của một tam giác- Bất đẳng thức tam giác.
Ngày dạy ..../......./ 2011
 A. Mục tiêu
-Học sinh nắm vững độ dài ba cạnh của một tam giác , từ đó biết được ba đoạn thẳng có độ dài như thế nào thì không thể là độ dài ba cạnh của một tam giác.
-Hs hiểu cách chứng minh định lý bất đẳng thức tam giác dựa trên quan hệ giữa ba cạnh và một góc trong một tam giác
-Bước đầu biết vận dụng bất đẳng thức tam giác để giải toán.
B. Chuẩn bị .
-Bảng phụ.
C. Các hoạt động trên lớp.
Hoạt động của thầy Hoạt động của trò
Hoạt động 1 : Kiểm tra (8').
-Gv nêu câu hỏi kiểm tra
a, Vẽ tam giác ABC có : Một Hs lên bảng kiểm tra.
BC = 6cm , AB = 4cm , AC = 5cm.	A
b, So sánh các góc trongABC.	 4cm	 5cm
	H	6cm
	B	C
 a, ABC có AB = 4cm , AC = 5cm , BC = 
 6cm AB < AC < BC.
 C < B < A ( quan hệ giữa góc và cạnh đối 
 diện trong tam giác).
b, Kẻ AHBC ( H BC). b, Xét ABH có H = 1v.
So sánh AB và BH ; AC và HC. AB > HB ( cạnh huyền lớn hơn cạnh góc 
 vuông).
 Tương tự với AHC có A = 1v.
 AC > HC.
Hoạt động 2 : Bất đẳng thức tam giác (18').
 Hoạt động của thầy Hoạt động của trò
Gv yêu cầu Hs làm ?1. - Hs toàn lớp thực hiện vào vở.
 Một Hs lên bảng thực hiện.
 Nhận xét : Không thể vẽ được tam giác có 
 độ dài ba cạnh như vậy.
Trong mỗi trường hợp , tổng độ dài hai
đoạn nhỏ so với đoạn lớn nhất như thế Hs : 1 + 2 < 4 ; 1 + 3 = 4 .
nào ?.
Như vậy không phải 3 độ dài nào cũng
 là độ dài 3 cạnh của một tam giác.
Gv yêu cầu Hs đọc định lý SGK Hs đọc định lý SGK.
Gv vẽ hình. A	 GT ABC
 KL AB + AC > BC.
 AB + BC > AC.
 B	C	 AC + BC > AB.
-Hãy cho biết GT-KL của định lý?.
Gv : Ta sẽ chứng minh bất đẳng thức 
đầu tiên.
-Làm thế nào để tạo ra một tam giác có Hs : Trên tia đối của tia AB lấy điểm D sao
một cạnh là BC , một cạnh là AB + AC cho AD = AC . Nối CD.
để so sánh chúng?. Có BD = BA + AC .
-Làm thế nào để chứng minh BD > BC? -Muốn chứng minh BD > BC ta cần có
- Tại sao BCD > BDC. BCD > BDC.
-Góc BDC bằng góc nào?. - Có A nằm giữa B và D nên tia CA nằm giữa 
 2 tia CB và CD nên BCD > ACD.
 Mà ACD cân do AD = AC.
 ACD = ADC ( = BDC ).
	 BCD > BDC.
Gv giới thiệu các bất đẳng thức ở phần 
kết luận của định lý được gọi là bất đẳng
 thức tam giác.
Hoạt động 3 : Hệ quả của bất đẳng thức tam giác(7').
-Hãy nêu lại các bất đẳng thức tam giác.
-Hãy áp dụng qui tắc chuyển vế để biến
đổi các bất đẳng thức trên ?.
-Hãy phát biểu hệ quả này bằng lời Hs : AB + BC > AC BC > AC - AB
Gv: Kết hợp với các bất đẳng thức tam AC + BC > AB BC > AB - AC.
giác ta có : Hs phát biểu hệ quả.
 AC - AB < BC < AC +AB
- Cho Hs làm ?3. Hs làm ?3.
Hoạt động 4 : Luyện tập- Củng cố(10').
-Hãy phát biểu nhận xét quan hệ giữa 3 Hs phát biểu nhận xét.
cạnh của một tam giác.
-Làm bài tập số 16/SGK. Hs làm bài tập 16.
 Có AC - BC < AB < AC + BC.
 7-1 < AB < 7 +1 .
	6 < AB < 8.
 mà độ dài AB là một số nguyên.
 AB = 7cm.
 ABC là tam giác cân đỉnh A.
Hoạt động 5 : Hướng dẫn về nhà (2').
-Nắm vững bất đẳng thức tam giác , học cách chứng minh định lý bất đẳng thức tam giác.
-Làm bài tập về nhà : 17,18,19/63 SGK.
 24,25/26 SBT.
HD : Bài tập 17/SGk
GV hđhs vẽ hình
? Để c/m MA + MB < IA+ IB Ta làm ntn ?
HS :So sánh MA với MI + IA
? Để so sánh MA với MI + IATa dựa vào tam giác nào ?
HS : dựa vào tam giác MIA
IV. Rút kinh nghiệm sau bài dạy
.................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................
TIếT 52 : Luyện tập
Ngày dạy ..../......./ 2011
A. Mục tiêu.
-Củng cố quan hệ giữa độ dài các cạnh của một tam giác. Biết vận dụng quan hệ này để xét xem ba đoạn thẳng cho trước có thể là độ dài ba cạnh của một tam giác không ?
-Rèn luyện kĩ năng vẽ hình theo đề bài , phân biệt giả thiết kết luận và vận dụng quan hệ giữa ba cạnh của một tam giác để chứng minh bài toán.
-Vận dụng quan hệ giữa ba cạnh của một tam giác vào thực tế cuộc sống.
B. Chuẩn bị .
-Bảng phụ , compa.
C. Các hoạt động trên lớp.
Hoạt động của thầy Hoạt động của trò
Hoạt động 1 : Kiểm tra chữa bài tập (12').
-Gv nêu yêu cầu kiểm tra. Hai Hs lên bảng kiểm tra.
Hs1 : Phát biểu nhận xét quan hệ giữa ba Hs1 : -Phát biểu nhận xét.
cạnh của một tam giác.
Chữa bài tập 18/63 SGK. - Chữa bài tập 18 SGK.
 a, 2cm ; 3cm ; 4cm.
 Có 4cm < 2cm + 3cm Vẽ được tam giác.
 b, 1cm ; 2cm ; 3.5cm
 Có 3.5cm > 1cm + 2cm Không vẽ được 
 tam giác.
 c, 2.2cm ; 2cm ; 4.2cm.
 Có 4.2cm = 2.2cm + 2cm Không vẽ được 
 tam giác.
Hs2 : Chữa bài tập 24/26 SBT. Hs2 :
	A	d
	C
	B
	C'
 C là giao điểm của đường thẳng d và đoạn 
 thẳng AB , nếu lấy C' là một điểm bất kì 
 thuộc đường thẳng d ( C' khác C ) . Nối C'A 
 C'B.
 Xét AC'B có AC' + C'B > AB ( bất đẳng 
 thức tam giác). 
 hay AC' + C'B > AC +CB ( vì C nằm giữa 
 A và B)
 CA + CB là nhỏ nhất.
Gv nhận xét và cho điểm. Hs nhận xét bài làm của bạn.
Hoạt động 2 : Luyện tập (22').
Bài 21/64 SGK.
Gv đưa đề bài lên bảng phụ Một Hs đọc đề bài.
Gv giới thiệu trên hình vẽ. Hs cả lớp suy nghĩ , áp dụng kết quả bài 24
-Trạm biến áp A. SBT trả lời bài toán: vị trí cột điện C phải
-Khu dân cư B. là giao của bờ sông với đường thẳng AB.
-Cột điện C.
-Cột điện C ở vị trí nào để độ dài AB là 
ngắn nhất?.
Gv vẽ hình lên bảng , yêu cầu Hs vẽ -Một Hs đọc đề bài.
hình vài vở. -Hs cả lớp vẽ hình vào vở.
 Một Hs nêu GT-KL của bài toán.
	A
 GT ABC ; M nằm trong ABC
	 BM.	
	I
 KL a, So sánh MA với MI + IA.
	M	 MA + MB < IB + IA.
	b, So sánh IB với IC + CB.
B	C IB + IA < CA + CB
Cho biết GT-KL của bài toán. c, MA + MB < CA + CB.
Gv yêu cầu Hs chứng minh miệng câu a Hs chứng minh câu a.
 a, Xét MAI có : 
 MA < MI + IA ( bất đẳng thức tam giác)
 MA + MB < MB + MI + IA.
 MA + MB < IA + IB (1).
 b, Xét IBC có : 
 IB < IC + CB ( bất đẳng thức tam giác ).
 IB + IA < IA + IC + CB.
 IB + IA < CA + CB (2).
 c, Từ (1) và (2) suy ra : 
 MA + MB < CA + CB.
Bài 26/27 SBT.	A
-Yêu cầu Hs đọc bài toán.
-Gv yêu cầu Hs vẽ hình và ghi GT-KL
của bài toán.
	B	C
	D
 GT ABC ; D nằm giữa B và C
 Kl AD < 
Gv gợi ý theo sơ đồ : Hs làm bài vào vở.
AD < Một Hs lên bảng trình bày.
 Xét ABD có : AD < AB + BD ( bất đẳng
2AD < AB + AC + BC thức tam giác).
 Tương tự với ACD có :
2AD < AB + AC + BD + DC AD < AC + DC.
 Do đó : Cộng vế theo vế ta có :
AD + AD < ( AB + BD ) + ( AC + DC). AD + AD < AB + BD + AC + DC.
Sau đó yêu cầu Hs trình bày bài chứng 2AD < AB + AC + BC.
minh. hay : AD < 
Hoạt động 3 : Bài tập thực tế (8').
Bài 22/64 SGK.
-Gv đưa đề bài lên bảng phụ , yêu cầu Hs hoạt động theo nhóm.
Hs hoạt động nhóm.	A
	 30km 90km
C
 (Máy phát)
 B
 ABC có:90-30 < BC < 90+30.
 60 < BC < 120.
 a, Nếu đặt tại C máy phát sóng truyền thanh 
 có bán kính phủ sóng 60km thì thành phố B 
 không nhận được tín hiệu.
 b,Nếu đặt tại C máy phát sóng truyền thanh 
 có bán kính phủ sóng là 120km thì thành 
 phố B luôn nhận được tín hiệu.
Hoạt động 4 : Hướng dẫn về nhà (3').
-Làm bài tập 25 đến 30/26-27 SBT.
-Mỗi Hs chuẩn bị cho tiết sau : Một tam giác bằng giấy ; một mảnh giấy kẻ ô vuông mỗi chiều 10 ô như hình 22 SGK.
IV. Rút kinh nghiệm sau bài dạy
..............................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................