Bài tập chương III Hình học Xạ ảnh
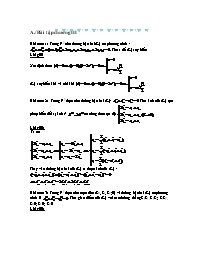
Trong P2 thực cho mục tiêu (S0, S1, S2;E). Viết phương trình đường bậc hai trong các trường hợp sau:
a. Đi qua S0, S1, S2,E
b. Đi qua S0, S1, S2,E và D(1:1:-1)
c.Đi qua A(0: 0: 1), B(0: 1: 1), C(1: 0: 1), D(2: -5 : 1)
Bạn đang xem tài liệu "Bài tập chương III Hình học Xạ ảnh", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
A./ Bài tập chương III
Bài toán 1: Trong P2 cho đương bậc hai (G) có phương trình :. Tìm a để (G) suy biến
Lời giải
Xét định thức
(G) suy biến khi và chỉ khi
Bài toán 2: Trong P2 thực cho đường bậc hai (G): . Tìm ảnh của (G) qua phép biến đổi xạ ảnh f: có công thức tọa độ
Lời giải:
Ta có
Thay vào đường bậc hai của (G) ta được ảnh của (G) :
Bài toán 3: Trong P2 thực cho mục tiêu (S0, S1, S2;E) và đường bậc hai (G) có phương trình là . Tìm giao điểm của (G) với các đường thẳng S0S1; S0S2; S1S2; S0E; S1E; S2E
Lời giải:
- Giao điểm (G) S0S1 xác định bởi:
Vậy: (G) S0S1=
- Giao điểm (G) S0S2 xác định bởi : chọn ta được hai giao điểm A (1:0:1) và B (1:0:-1)
- Giao điểm (G) S1S2 khi đó ta được hai điểm C(0:1:1) và D(0:1:-1)
- Giao điểm (G) S0E là điểm C(0:1:1)
- Giao điểm (G) S1E là điểm H (1:0:1)
- Giao điểm (G) S2E là hai điểm M(1:1:) và N(1:1:-)
Bài toán 4: Trong P2 thực cho mục tiêu (S0, S1, S2;E). Viết phương trình đường bậc hai trong các trường hợp sau:
a. Đi qua S0, S1, S2,E
b. Đi qua S0, S1, S2,E và D(1:1:-1)
c.Đi qua A(0: 0: 1), B(0: 1: 1), C(1: 0: 1), D(2: -5 : 1)
Lời giải:
Phương trình bậc hai (G) có dạng:
a. Thay tọa độ S0, S1, S2 vào (G) ta được :
Vậy: (G) có dạng:
b. Thay tọa độ S0, S1, S2,E và D(1:1:-1) vào (G) ta được:
Vậy: (G) có dạng:
c. Thay tọa độ các điểm A(0: 0: 1), B(0: 1: 1), C(1: 0: 1), D(2: -5 : 1) vào (G) ta được :
Vậy : (G) có dạng :
Bài toán 5: Trong P2 thực cho các đường bậc hai có phương trình
a.
b.
c.
Gọi tên các đường bậc hai trên
Lời giải:
Đặt ( cặp đường thẳng ảo liên hợp)
Đặt : Cặp đường thẳng trùng nhau
Đặt : ( cặp đường thẳng ảo liên hợp)
Bài toán 6: Trong P3 thực cho các mặt bậc hai có phương trình
a.
b.
c.
Gọi tên các đường bậc hai trên
Lời giải:
Đặt: (vậy (G) là mặt nón)
Bài toán 7: Trong P2 thực cho mục tiêu (S0, S1, S2;E) và đường bậc hai (G) có phương trình:
Viết phương trình đường đối cực của các điểm S0, S1, S2, E
Tìm cực của đường thẳng (d):
Gọi tên của (G)
Lời giải:
Ta có:
a. Đối cực với S0 đường thẳng (do): (u0: u1: u2) = (2:4:0)
với
(d0):
Tương tự
- Đối cực S1 (0:1:0) là đường thẳng (d2) (u0: u1: u2) = (4:4:-6)
(d1):
- Đối cực S2 (0:0:1) là đường thẳng (d2) (u0: u1: u2) = (0:-6:-4)
(d2):
- Đối cực E (1:1:1) là đường thẳng (d3) (u0: u1: u2) = (6:2:-10)
(d3):
Tìm cực của đường thẳng (d):
Xét đường thẳng (d): có u(1:1:-1)
Tọa độ của đường thẳng (d) là nghiệm của phương trình sau:
Vậy cực của đường thẳng (d) là điểm A
Đặt: Khi đó (S): là oval thực
Bài toán 8: Trong P2 cho đường bậc hai (G) có phương trình:
a. Chứng minh rằng hai điểm A(1:0:0), B (1:1:0) liên hợp với nhau đối với (G)
b. Tìm cực D của đường AB
c. Cho E’ (1:0:1). Chứng minh rằng (A, B, D; E) là một mục tiêu và viết phương trình của (G) đối với mục tiêu đó.
Lời giải:
Với A(1:0:0), B (1:1:0) ta có
Vạy hai điểm A,B liên hợp với (G)
b/. ;
Đối cự với điểm A là đường thẳng (d1):
Tương tự ta có: ; ;
Vậy đối cực với điểm B là đường thẳng (d2):
Do đó, đối cực D của AB là giao của hai đường thẳng (d1) và (d2) có tạo D (0:1:1)
Đặt
Xét Vậy {A,B,D} độc lập tuyến tính
Và E’= 2A-B+D nên là mục tiêu của P2. Gọi là cơ sở đại diện cho mục tiêu đã cho. Ta có cơ sở đại diện cho mục tiêu (A,B,D;E’) là
Khi đó ta có:
Ta có công thức đổi tọa độ là:
Thay vào (G) ta được ta được phương trình của (G) đối với mục tiêu đó là:
Bài toán 9: Trong P3 thực cho mặt bậc hai (G) có phương trình
a. Tìm điểm kì dị của (G)
b. Tìm đối cực của điểm A (1:0:0:0 ) đối với (G)
c. Tìm giao (G) .
Lời giải:
Tạo độ điểm kì dị là nghiệm của phương trình sau:
Vậy : M (1:0:1:0) là điểm kì dị
b. Mặt đối cực điểm A (1:0:0:0 ) đối với (G) là :
c.Giao điểm (G) xác định bởi:
Vậy: (G) là hai đường thẳng (d1): và (d2):
B./ ĐỊNH LÍ PASCAL
Hình 6 đỉnh
Tập hợp 6 điểm phân biệt theo thứ tự A1, A2, A3 ,A4 ,A5, A6 gọi là hình 6 đỉnh.
Kí hiệu : A1A2A3A4A5A6 . Các Ai gọi là đỉnh của hình sáu đỉnh đó. Các cạnh là A1A2, A2A3, A3A4, A4A5, A5A6 , A6 A1 . Các đỉnh đối diện là: A1 và A4 ; A2và A5; A3 và A6. Các cạnh đối diện là : A1A2 và A4A5; A2A3 và A5A6 ; A3A4 và A6 A1.
2/ Định lí Pascal ( Về hình 6 đỉnh)
Cho các điểm cùng thuộc một ovan hay nội tiếp ovan(có thể hoán đổi thứ tự). Gọi .
Khi đó các điểm thẳng hàng.
Chứng minh.
Giả sử hình 6 đỉnh ABCDEF nội tiếp ôvan (S). Ta kí hiệu:
P = AB DE; Q = BCEF; R= CDFA; M = ABCD; N =BC DE. Khi đó ta chứng minh P, Q, R thẳng hàng
- Từ định lý Stayne đảo, ta có.
=
Nhưng: =
=
Vì vậy ta có: =
Chứng tỏ có một phép ánh xạ ảnh f: mà f(M) = B, f(C) = C, f(D) = N, f(Q) =R. Hơn thế f là phép xuyên tâm ( vì C tự ứng)
Suy ra: MB , DN, QR đồng quy. (hay P, Q, R thẳng hàng).
Định lý đảo Pascal (Định lý Pascal đảo tổng quát do Braikenridge, Maclaurin)
- Nếu một lục giác có giao điểm các cặp cạnh đối cùng nằm trên một đường thẳng thì lục giác đó nội tiếp một conic
Trong trường hợp conic là đường tròn, định lý được phát biểu:
- Nếu một lục giác có giao điểm các cặp cạnh đối thẳng hàng và năm trong sáu đỉnh cùng nằm trên đường tròn thì đỉnh còn lại của lục giác đó cũng nằm trên đường tròn đó.
Chứng minh:
- Xét lục giác ABCDEF có A, B, C, D, E cùng nằm trên (O) và AB ∩ DE = {M}, BC ∩ DF = {N}, CD ∩ AF = {P}
- Theo giả thiết M, N, P thẳng hàng.
Vậy CD ∩ MN = {P}
EF ∩ (O) = {D;F’}, CD ∩ AF’ = {P’}
Lục giác ABCDEF’ nội tiếp (O)
Theo định lý Pascal: M, N, P’ thẳng hàng
CD ∩ MN = {P’} => P ≡ P’ => F ≡ F’
Ta có thể viết lại định lý Pascal với đường tròn như sau:
Xét lục giác có 5 trong 6 đỉnh cùng nằm trên đường tròn.
Đỉnh còn lại của lục giác cũng thuộc đường tròn đó
Giao điểm các cặp cạnh đối của lục giác thẳng hàng.
4. Các trường hợp đạc biệt cùa định lý Pascal
Ta có thể định nghĩa hình 5 đỉnh, 4 đỉnh, 3 định tương tự định nghĩa hình 6 đỉnh
4.1 Định lý Pascal: ( hình 5 đỉnh)
Nếu hình 5 đỉnh ABCDE nội tiếp ovan (S)thì 3 giao điểm của cạnh AB với cạnh EF, cạnh BC với tiếp tuyến của (S) tại F, cạnh CD với cạnh FA thảng hàng
4.2 Định lý Pascal: (hình 4 đỉnh)
Nếu một hình 4 đỉnh ABCD nội tiếp một đường ovan thì giao điểm các cặp cạnh đối diện và giáo điểm các tiếp tuyến tại các cặp đỉnh đối diện là 4 điểm thẳng hàng
4.3 Định lý Pascal ( hình 3 đỉnh)
- Nếu một hình 3 đỉnh nội tiếp một ovan thì giao điểm của cạnh với tiếp tuyến tại đỉnh đối diện là 3 điểm thẳng hàng.
5./ Một số bài tập áp dụng
Bài toán 1: (Định lý Newton)
(Hình 1)
Một đường tròn nội tiếp tứ giác lần lượt tiếp xúc với các cạnh tại . Khi đó các đường thẳng đồng quy.
Lời giải:
Gọi .
Vì là giao điểm của các tiếp tuyến với đường tròn tại áp dụng
định lý Pascal cho các điểm , ta có:
Suy ra thẳng hàng.
Áp dụng định lý Pascal cho các điểm ta có:
Hình 1
Suy ra thẳng hàng.
Từ đó ta được thẳng hàng.
Vậy đồng quy tại .
Chứng minh tương tự đối với đường thẳng ta được điều phải chứng minh.
Bài toán 2:
Cho tam giác nội tiếp trong một đường tròn. Gọi lần lượt là các điểm chính giữa của các cung ; là điểm tuỳ ý trên cung ; .
(Hình 2)
Chứng minh rằng đường thẳng chứa tâm của đường tròn nội tiếp tam giác .
Hình 2
Lời giải:
Vì lần lượt là điểm chính giữa của các cung nên theo thứ tự là các đường phân giác của góc .
Suy ra
Áp dụng định lý Pascal cho sáu điểm ta có:
;
Vậy thẳng hàng.
Bài toán 3:
Cho tam giác ABC nội tiếp đường tròn (O), đường cao đỉnh A, B, C lần lượt cắt (O) tại A’, B’, C’. D nằm trên (O), .
(Hình 3)
Chứng minh rằng: A”, B”, C”, trực tâm H thẳng hàng.
Lời giải:
Áp dụng định lý Pascal cho sáu điểm ta có:
Vậy thẳng hàng.
Tương tự suy ra A”, B”, C”, H thẳng hàng.
Hình 3
Bài toán 4:
Ngũ giác ABCDE lồi thỏa mãn: . Điểm F trong đoạn AB sao cho
(Hình 4)
Chứng minh rằng: A, G ,B thẳng hàng
Lời giải:
Gọi , Q, R lần lượt là giao điểm của AD và BD với đường tròn đường kính PD, .
Áp dụng định lý Pascal cho sáu điểm ta có:
Vậy thẳng hàng.
Bài toán 5: (Định lý Brianchon)
Lục giác ABCDEF ngoại tiếp một đường tròn.
(Hình 5)
Khi đó AD, BE, CF đồng quy.
Lời giải:
Gọi các tiếp điểm trên các cạnh lần lượt là G, H, I, J, K, L. Khi đó GH, HI, IJ, JK, KL, LG lần lượt là đối cực của B, C, D, E, F, A.
Gọi
Hình 5
Theo Pascal cho lục giác GHIJKL ta có M, N, P thẳng hàng.
Mà M, N, P lần lượt là đối cực của AD, BE, CF nên suy ra AD, BE, CF đồng quy tại cực của đường thẳng MNP.
Bài toán 6:
Cho tam giác ABC nội tiếp đường tròn (O), đường cao đỉnh A, B, C lần lượt cắt (O) tại A’, B’, C’. D nằm trên (O), .
(Hình 6)
Chứng minh rằng: A”, B”, C”, trực tâm H thẳng hàng.
Lời giải:
Áp dụng định lý Pascal cho sáu điểm ta có:
Vậy thẳng hàng.
Hình 6
Tương tự suy ra A”, B”, C”, H thẳng hàng.
Tài liệu đính kèm:
 bt hinh hoc xa anh.doc
bt hinh hoc xa anh.doc





