Bồi dưỡng Hình học 7 - Trường THCS Xuân Hoà

Tiết 10 – 12 tổng ba góc trong tam giác 
NG: ..........................
I/ Mục tiêu:
- Giúp HS củng cố kiến thức tổng 3 góc trong tam giác, góc ngoài của tam giác
- Rèn kĩ năng chứng minh hình học
II/ Tiến trình dạy học:
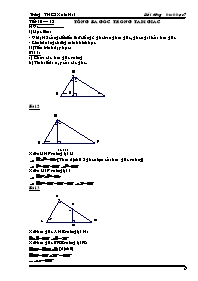
Bài 1:
a) Chỉ ra các tam giác vuông
b) Tính số đo x, y của các góc.
Bài 2
 Hình 57
Xét MNP vuông tại M
 (Theo định lí 2 góc nhọn của tam giác vuông)
Xét MIP vuông tại I
Bài 3
Xét tam giác AHE vuông tại H:
Xét tam giác BKE vuông tại K:
 (định lí)
 Bài 4
GT
Tam giác ABC vuông tại A
KL
a, Các góc phụ nhau
b, Các góc nhọn bằng nhau 
a) Các góc phụ nhau là: và 
b) Các góc nhọn bằng nhau 
 (vì cùng phụ với )
 (vì cùng phụ với )
Tiết 13 – 15 hai tam giác bằng nhau 
NG: ..........................
I/ Mục tiêu:
- Giúp HS củng cố kiến thức các TH bằng nhau của tam giác.
- Rèn kĩ năng chứng minh hình học.
II/ Tiến trình dạy học:
Bài 1:
Vẽ tam giác biết ba cạnh )
- Vẽ 1 trong 3 cạnh đã cho, chẳng hạn vẽ BC = 4cm.
- Trên cùng một nửa mặt phẳng vẽ 2 cung tròn tâm B và C.
- Hai cung cắt nhau tại A
- Vẽ đoạn thẳng AB và AC ta được ABC
Bài 2:
GT
ADE và BDE có AD = BD; AE = EB
KL
a) ADE = BDE
b) 
a) Xét ADE và BDE có: AD = BD; AE = EB (gt) DE chung
ADE =BDE (c.c.c)
b) Theo câu a: ADE = BDE
 (2 góc tơng ứng)
Bài 3:
GT
AB = 4cm
(A; 2cm) và (B; 3cm) cắt nhau tại C và D
KL
AB là tia phân giác góc CAD
Xét ACB và ADB có:
AC = AD (= 2cm)
BC = BD (= 3cm)
AB là cạnh chung
 ACB = ADB (c.c.c)
AB là tia phân giác của góc CAD
Bài 4:
 Cho ABC = DEF. Biết . Tính các góc còn lại của mỗi tam giác.
ABC = DEF 
 mà 
Xét ABC có: 
Bài 5:
Vẽ tam giác biết hai cạnh và góc xen giữa 
- Vẽ 
- Trên tia Bx lấy điểm A: BA = 2cm
- Trên tia By lấy điểm C: BC = 3cm
- Vẽ đoạn AC ta được ABC
Bài 6:
Cho hình vẽ, chứng minh 
Xét ACD và BDC 
có AC = BD (gt)
AD = BC (gt)
DC chung
 ACD = BDC (c.c.c) 
Bài 7:
 H. 82 H. 83
 H. 84
H.82: ABD = AED (c.g.c) vì AB = AE (gt); (gt); cạnh AD chung
H.83: GHK = KIG (c.g.c) vì (gt); IK = HG (gt); GK chung
H.84: Không có tam giác nào bằng nhau 
Bài 8:
a) ABC = ADC
đã có: AB = AD; AC chung
thêm: 
b) AMB = EMC
đã có: BM = CM; 
thêm: MA = ME
c) CAB = DBA
đã có: AB chung; 
thêm: AC = BD
	-------------------------------------------------
Tiết 16 – 18 hai tam giác bằng nhau 
NG: ..........................
I/ Mục tiêu:
- Giúp HS củng cố kiến thức các TH bằng nhau của tam giác.
- Rèn kĩ năng chứng minh hình học.
II/ Tiến trình dạy học:
Bài 9:
DKE có 
mà ( theo đl tổng 3 góc của tam giác) 
 Xét ABC và KDE có:
 AB = KD (gt)
 BC = DE (gt)
 ABC = KDE (c.g.c)
Bài 10:
GT
; BAx; DAy; AB = AD
EBx; CAy; AE = AC
KL
ABC = ADE
Xét ABC và ADE có:
 AB = AD (gt)
 chung
 ABC = ADE (c.g.c)
Bài 11
GT
ABC vàA'BC
 BC = 3cm, CA = CA' = 2cm
KL
ABC A'BC
Góc ABC không xen giữa AC, BC, không xen giữa BC, CA'
Do đó không thể sử dụng trường hợp cạnh-góc-cạnh để kết luận ABC = A'BC 
Bài 12
GT
IA = IB, d AB tại I
 M d
KL
So sánh MA , MB
*TH1: M I AM = MB
*TH2: M I:
Xét AIM, BIM có:
 AI = IB (gt)
 (gt)
 MI chung
 AIM = BIM (c.g.c)
 AM = BM
Bài 13
GT
AH = HK, AK BC
KL
Tìm các tia phân giác
* Xét ABH vàKBH
 =900
 AH = HK (gt),
 BH là cạnh chung
 => ABH =KBH (c.g.c)
 Do đó (2 góc tương ứng). 
 BH là phân giác của .
GT
OA = OB
KL
AC = BD
Bài 14
Xét OBD và OAC Có:
OA = OB
chung
 OAC = OBD (g.c.g)
 BD = AC
Bài 15
DEF: 
 => 
 ABC = FDE (g.c.g) vì
Bài 16
GT
AB // CD
 AC // BD
KL
AB = CD
AC = BD
Nối A với D.
Xét ABD và DCA có:
 (hai góc so le trong)
 AD là cạnh chung
 (hai góc so le trong)
 ABD = DCA (g.c.g)
 AB = CD, BD = AC
	-------------------------------------------------
Tiết 19 – 21 hai tam giác bằng nhau (TT)
NG: ..........................
I/ Mục tiêu:
- Giúp HS củng cố kiến thức các TH bằng nhau của tam giác.
- Rèn kĩ năng chứng minh hình học.
II/ Tiến trình dạy học:
Bài 1: Cho ABC có góc A bằng 600. Tia phân giác của góc B cắt AC ở M, tia phân giác của góc C cắt AB ở N. Chứng minh rằng BN + CM = BC.
Bài 2: Cho ABC vuông tại A, M là trung điểm của AC. Trên tia đối của tia MB lấy điểm K sao cho MK = MB. Chứng minh rằng:
KC vuông góc với AC.
AK song song với BC.
Bài 3: Cho ABC, kẻ BD vuông góc với AC, kẻ CE vuông góc với AB. Trên tia đối của tia BD, lấy điểm H sao cho BH = AC. Trên tia đối của tia CE lấy điểm K sao cho CK = AB. Chứng minh rằng AH = AK.
Bài 4: Cho ABC có AB = AC. Trên cạnh AB và AC lấy các điểm D và E sao cho AD = AE. Gọi K là giao điểm của BE và CD. Chứng minh rằng:
a) BE = CD b) KBD = KCE. 
Bài 5: Cho ABC có góc A = 600. Tia phân giác của góc B cắt AC ở D, tia phân giác của góc C cắt AB ở E. Các tia phân giác đó cắt nhau ở I. Chứng minh rằng ID = IE.
Bài 6: Cho đoạn thẳng AB, O là trung điểm của AB. Trên cùng một nửa mặt phẳng bờ AB, vẽ các tia Ax và By vuông góc với AB. Gọi C là một điểm thuộc tia Ax. Đường vuông góc với OC tại O cắt tia By tại D. Chứng minh rằng: CD = AC + BD.
Bài 7: Trên cạnh BC của ABC, lấy các điểm E và F sao cho BE =CF. Qua E và F vẽ các đường thẳng song song với BA, chúng cắt cạnh AC theo thứ tự ở G và H. Chứng minh rằng: EG + FH = AB.
Bài 8: Cho ABC vuông tại A, AB = AC. Qua A vẽ đường thẳng d sao cho B và C nằm cùng phía đối với đường thẳng d. Kẻ BH và CK vuông góc với d. Chứng minh rằng:
a) AH = CK b) HK = BH + CK 
Bài 9: Cho ABC. Gọi M là trung điểm của AC, N là trung điểm của AB. Trên tia đối của tia MB lấy điểm E sao cho ME = MB, trên tia đối của tia NC lấy điểm F sao cho NF = NC. Chứng minh rằng:
a) MAE = MCB.
b) AE = AF.
c) Ba điểm A, E, F thẳng hàng. 
Bài 10: Cho đoạn thẳng AB, D là trung điểm của AB. Kẻ Dx vuông góc với AB. Trên Dx lấy hai điểm M và N (M nằm giữa D và N). Chứng minh rằng:
a) NAD = NBD.
b) MNA = MNB.
c) ND là phân giác của góc ANB.
d) Góc AMB lớn hơn góc ANB.
-----------------------------------
Tiết 22 – 24 luyện tập 
NG: ..........................
I/ Mục tiêu:
- Giúp HS củng cố kiến thức: tam giác cân, đinh lí Pitago
- Rèn kĩ năng chứng minh hình học.
II/ Tiến trình dạy học:
Bài 1: a) Cho ABC cân tại A, BD và CE là các đường phân giác của B và C. Chứng minh rằng BD = CE.
b) Chứng minh trong một tam giác cân, hai đường cao ứng với các cạnh bên thì bằng nhau.
Bài 2: Cho tam giác ABC cân tại A. Trên cạnh BC lấy hai điểm D và E sao cho BD = CE. Nối AD và AE.
Chứng minh ADE cân.
Chứng minh ABE = ACD.
Bài 3: Cho góc xOy. Trên Ox lấy điểm A và trên tia đối của tia Oy lấy điểm B sao cho OA = OB. Chứng minh rằng AB song song với tia phân giác của góc xOy.
Bài 4: Cho ABC cân tại A. Trên cạnh BA lấy điểm D, sao cho A là trung điểm của BD. Chứng minh rằng:
a) BCD = ABC + ADC b) BCD = 900
Bài 5: Cho ABC đều. Trên tia AB lấy điểm D sao cho B là trung điểm của AD.
Chứng minh rằng BCD cân.
Tính các góc của BCD.
Bài 6: Cho ABC (AB = AC). Trên nửa mặt phẳng chứa điểm C có bờ là đường thẳng AB, ta kẻ tia Bx song song với AC. Chứng minh rằng tia BC là tia phân giác của góc ABx.
Bài 7: Cho ABC. Vẽ các tam giác đều ABD và ACE ra phía ngoài ABC. Nối BE và CD. Gọi M là N là trung điểm của BE và CD. Chứng minh AMN đều.
Định lý Py-ta-go
Bài 1: Tam giỏc ABC cú gúc A tự, = 300; AB = 29, AC = 40. Vẽ đường cao AH, tớnh BH.
Bài 2: Tam giỏc ABC cú AB = 25, AC = 26, đường cao AH = 24. Tớnh BC.
Về nhà
Bài 8: Cho ABC cân, AB là cạnh đáy, góc C bằng 1000. Trên nửa mặt phẳng chứa điểm C, bờ là đường thẳng AB, dựng tia Ax tạo với AB một góc 300 và tia By tạo với tia BA một góc 200. Hai tia Ax và By cắt nhau tại D. Tính góc ACD.
Bài 9: Cho ABC cân tại A có góc A nhỏ hơn 900, kẻ BD vuông góc với AC. Trên cạnh AB lấy điểm E sao cho AE = AD. Chứng minh rằng:
DE song song với BD.
CE vuông góc với AB.
Bài 10: Trên cạnh huyền BC của tam giác vuông ABC, lấy các điểm D và E sao cho BD = BA, CE = CA. Tính góc DAE.
-----------------------------------
Tiết 25 – 27 luyện tập 
NG: ..........................
I/ Mục tiêu:
- Giúp HS củng cố kiến thức: tam giác cân, đinh lí Pitago
- Rèn kĩ năng chứng minh hình học.
II/ Tiến trình dạy học:
Bài 11: Cho điểm M thuộc đoạn thẳng AB. Trên cùng một nửa mặt phẳng bờ AB, vẽ các tam giác đều AMC, BMD. Gọi E và F theo thứ tự là trung điểm của AD và CB. Chứng minh rằng MEF đều.
Bài 12: Cho ABC cân tại A, có góc A bằng 1200, BC = 6cm. Đường vuông góc với AB tại A cắt BC ở D. Tính độ dài BD.
Bài 13: Cho ABC cân tại, có góc A bằng 1200. Trên tia phân giác của góc A, lấy điểm E sao cho AE = AB + AC. Chứng minh rằng BCE đều.
Bài 14: Cho ABC có góc các góc nhỏ hơn 1200. Vẽ ở phía ngoài ABC các tam giác đề ABD, ACE. Gọi M là giao điểm của DC và BE. Chứng minh rằng:
a) Góc BMC bằng 1200 b) góc AMB = 1200
Bài 15: ABC cân tại A, góc A bằng 1400. Trên nửa mặt phẳng bờ BC chứa điểm A, kẻ tia Cx sao cho góc ACx = 1100. Gọi D là giao điểm của các tia Cx và BA. Chứng minh rằng AD = BC.
Bài 16: Cho tam giác đều ABC.
a) Hãy vẽ điểm O cách đều ba đỉnh A, B, C.
b) Trên tia đối của tia AB lấy một điểm D, trên tia đối của tia BC lấy một điểm E, trên tia đối của tia CA lấy một điểm F sao cho: AD = BE = CF. Chứng minh rằng tam giác DEF là tam giác đều và điểm O cách đều ba đỉnh D, E, F. 
Định lý Py-ta-go
Bài 3: Độ dài cỏc cạnh gúc vuụng của một tam giỏc vuụng tỉ lệ với 8 và 15, cạnh huyền dài 51cm. Tớnh độ dài hai cạnh gúc vuụng.
Bài 4: Cho tam giỏc ABC vuụng tại A, đường cao AH, trờn đú lấy điểm D. Trờn tia đối của tia HA lấy một điểm E sao cho HE = AD. Đường thẳng vuụng gúc với AH tại D cắt AC tại F. Chứng minh rằng EB ^ EF.
Về nhà:
Bài 17: Cho tam giác ABC (AB = AC). Hai đường cao AI và BK cắt nhau ở điểm H.
a) Chứng minh rằng tam giác BHC cân.
b) Bây giờ cho góc BAC = 200. Tính góc BHC. 
(HD a. HB = HC b. 1600)
Bài 18: Cho tam giác ABC (AB = AC). Trên tia đối của tia BC lấy điểm D sao cho BD = AB và trên tia đối của tia CB lấy điểm E sao cho CE = AC.
a) Chứng minh rằng tam giác ADE cân.
b) Bây giờ cho góc BAC có số đo bằng 400. Tìm số đo các góc của tam giác ADE.
(HD a. AD = AE b. 350; 1100; 350)
Bài 19: Cho tam giác ABC biết độ dài cạnh BC gấp đôi độ dài đường trung tuyến AM.
a) Tính số đo góc BAC.
b) Gọi MD là đường phân giác của góc AMC. Chứng minh: MD//AB.
Bài 20: Cho tam giác ABC cân tại A. Trên tia đối của tia CA lấy một điểm D nào đó.
a) Chứng minh rằng: ABD = 2CBD + CDB.
b) Bây giờ cho góc A bằng 300 và góc ABD = 900. Tính góc CBD. (ĐS: 150)
-----------------------------------
Tiết 28 – 30 các trường hợp bằng nhau 
của tam giac vuông
NG: ..........................
I/ Mục tiêu:
- Giúp HS củng cố kiến thức về các trường hợp bằng nhau của tam giác vuông.
- Rèn kĩ năng chứng minh hình học.
II/ Tiến trình dạy học:
Bài 1: Cho  ... ho D ABC cõn tại A, đường cao AH. Trờn tia đối của tia AH lấy điểm D sao cho HD = HA. Trờn tia đối của tia CBlấy điểm E sao cho CE = CB
	a/ Chứng minh rằng C là trọng tõm của D ADE
	b/ Tia AC cắt DE tại M. Chứng minh rằng AE// HM.
Bài 5: Cho D ABC, O là một điểm nằm trong tam giỏc. Vẽ BH và CK vuụng gúc đường thẳng AO. Cho biết cỏc tam giỏc AOB, BOC, COA cú diện tớch bằng nhau, chứng minh rằng:
	a/ BH = CK
	b/ O là trọng tõm của D ABC
-----------------------------------
Tiết 46 – 48 các đường đồng quy
trong tam giác (TT)
NG: ..........................
I/ Mục tiêu:
- Giúp HS củng cố kiến thức đã học: Tớnh chất tia phõn giỏc của một gúc. Tớnh chất ba đường phõn giỏc của tam giỏc
- Rèn kĩ năng chứng minh hình học.
II/ Tiến trình dạy học:
Bài 1: Cho D ABC, Â = 1200, phõn giỏc AD, BE, CF. Tớnh chu vi DDEF biết DE = 21, DF = 20.
Bài 2: Cho gúc xOy. Lấy điểm A trờn tia Ox, điểm B trờn tia Oy. Vẽ cỏc tia phõn giỏc của cỏc gúc BAx và ABy cắt nhau tại M. Từ M vẽ một đường thẳng vuụng gúc với OM, cắt Ox, Oy lần lượt tại C và D. Chứng minh rằng D ACD cõn.
Bài 3: Cho DABC, , phõn giỏc BD, CE. Đường thẳng chứa tia phõn giỏc ngoài tại đỉnh A của D ABC cắt đường thẳng BC tại F. Chứng minh rằng:
	a/ ADF = BDF
	b/ Ba điểm D, E, F thẳng hàng.
Bài 4: Cho DABC, cỏc tia phõn giỏc gúc B và gúc C cắt nhau tại O. Từ A vẽ một đường thẳng vuụng gúc với OA, cắt cỏc tia BO và CO lần lượt tại M và N. Chứng minh rằng BM ^ BN và CM ^ CN.
Bài 5: Cho DABC, , đường cao AH, phõn giỏc BD. Cho biết gúc BDA = 450. chứng minh rằng HD// AB
Bài 6: Cho D ABC vuụng gúc tại A, AB =3, AC = 4. Phõn giỏc gúc B, gúc C cắt nhau tại O. Vẽ OE ^ AB; OF ^ AC.
	a/ Chứng minh rằng AB + AC - BC = 2AE
	b/ Tớnh khoảng cỏch từ O tới đỉnh cỏc cạnh của D ABC
	c/ Tớnh OA, OB, OC
-----------------------------------
Tiết 49 – 51 các đường đồng quy
trong tam giác (TT)
NG: ..........................
I/ Mục tiêu:
- Giúp HS củng cố kiến thức đã học: Tớnh chất đường trung trực của một đoạn thẳng. Tớnh chất ba đường trung trực của tam giỏc
- Rèn kĩ năng chứng minh hình học.
II/ Tiến trình dạy học:
Bài 1: Cho D ABC cõn tại A. Trờn cỏc cạnh AB và AC lần lượt lấy cỏc điểm M và N sao cho AM + AN = AB.
	a/ Đường trung trực của AB cắt tia phõn giỏc của gúc A tại O. Chứng minh rằng D BOM = D AON
	b/ Chứng minh rằng khi M và N di động trờn hai cạnh AB và AC nhưng vẫn cú AM + AN = AB tbỡ đường trung trực của MN luụn đi qua một điểm cố định.
Bài 2: Cho gúc xOy = a0, A là một điểm di động ở gúc trong gúc đú. Vẽ cỏc điểm M và N sao cho đường Ox là đường trung trực của AM, đường thẳng Oy là đường trung trực của AN.
	a/ Chứng minh rằng đường trung trực của MN luụn đi qua một điểm cố định.
	b/ Tớnh giỏ trị của a để O là trung điểm của MN
Bài 3: Cho gúc vuụng xOy và A là một điểm cố định ở trong gúc đú. Một gúc vuụng đỉnh A quay quanh A, cú hai cạnh cắt Ox, Oy lần lượt tại B và C. Gọi M là trung điểm của BC. Chứng minh rằng M luụn di động trờn một đường thẳng cố định.
Bài 4: Cho D ABC khụng vuụng. Cỏc đường trung trực của AB và AC cắt nhau tại O, cắt đường thẳng BC theo thứ tự tại M và N. Chứng minh rằng tia AO là tia phõn giỏc của gúc MAN.
Bài 5: Cho D ABC. Trờn tia BA lấy một điểm M, trờn tia CA lấy một điẻm N sao cho BM + CN = BC. Chứng minh rằng đường trung trực của MN luụn đi qua một điểm cố định .
-----------------------------------
Tiết 52 – 54 các đường đồng quy
trong tam giác (TT)
NG: ..........................
I/ Mục tiêu:
- Giúp HS củng cố kiến thức đã học: Tớnh chất 3 đường cao của tam giỏc
- Rèn kĩ năng chứng minh hình học.
II/ Tiến trình dạy học:
Bài 1: Cho D ABC vuụng cõn tại B. Trờn cạnh AB lấy một điểm H sao cho . Trờn tia đối của tia BC lấy điểm K sao cho BK = BH. Tớnh gúc AKH.
Bài 2: Cho tam giỏc nhọn ABC, hai đường cao BD, CE gặp nhau tại H. Vẽ điểm K sao cho AB là trung trực của HK. Chứng minh rằng gúc KAB = gúc KCB.
Bài 3: Tam giỏc ABC cú cạnh BC là cạnh lớn nhất. Trờn cạnh Bc lấy cỏc điểm D và E sao cho BD = BA và CE = CA. Tia phõn giỏc của gúc B cắt AE tại M; tia phõn giỏc của gúc C cắt AD tại N. Chứng minh rằng tia phõn giỏc của gúc BAC vuụng gúc với MN.
Bài 4: Cho DABC cõn tại A, Â = 300; BC = 2. Trờn cạnh AC lấy điểm D sao cho AD = .
	a/ Tớnh gúc ABD
	b/ So sỏnh ba cạnh của D DBC
-----------------------------------
Tiết 55 – 57 các đường đồng quy
trong tam giác (TT)
NG: ..........................
I/ Mục tiêu:
- Giúp HS củng cố kiến thức đã học: Tớnh chất 3 đường cao, p/g, trung tuyến, trung trực của tam giỏc
- Rèn kĩ năng chứng minh hình học.
II/ Tiến trình dạy học:
Bài 1: Cho D ABC cõn tại A, Â= 1080. Gọi O là giao điểm của cỏc đường trung trực, I là giao điểm của cỏc tia phõn giỏc. Chứng minh rằng BC là đường trung trực OI.
Bài 2: Cho D ABC cú , phõn giỏc AD. Trờn AD lấy điểm O. Trờn tia đối của tia AC lấy điểm M sao cho gúc ABM = gúc ABO. Trờn tia đối của tia AB lấy một điểm N sao cho gúc CAN = gúc ACO. Chứng minh rằng:	
	a/ AM = AN
	b/ D MON là tam giỏc đều
Bài 3: Cho D ABC cõn tại A, cạnh đỏy nhỏ hơn cạnh bờn. Đường trung trực của AC cắt đường thẳng BC tạiM. Trờn tia đúi của tia AM lấy điểm N sao cho AN = BM
	a/ Chứng minh rằng gúc AMC = gúc BAC
	b/ Chứng minh rằng CM = CN
	c/ Muốn cho CM ^ CN thỡ tam giỏc cõn ABC cho trước phải cú thờm điều kiện gỡ?
-----------------------------------
Tiết 58 – 60 ôn tập 
NG: ..........................
I/ Mục tiêu:
- Giúp HS củng cố kiến thức đã học.
- Rèn kĩ năng chứng minh hình học.
II/ Tiến trình dạy học:
BÀI 1). Cho gúc nhọn xOy. Điểm H nằm trờn tia phõn giỏc của gúc xOy. Từ
H dựng cỏc đường vuụng gúc xuống hai cạnh Ox và Oy (A thuộc Ox và B thuộc Oy).
a) Chứng minh tam giỏc HAB là tam giỏc cõn
b) Gọi D là hỡnh chiếu của điểm A trờn Oy, C là giao điểm của AD với OH. Chứng minh BC ⊥ Ox.
c) Khi gúc xOy bằng 600, chứng minh OA = 2OD.
BÀI 2)Cho ∆ABC vuụng ở C, cú Aˆ = 600 , tia phõn giỏc của gúc BAC
cắt BC ở E, kẻ EK vuụng gúc với AB. (K AB), kẻ BD vuụng gúc AE (D AE).
Chứng minh a) AK=KB b) AD=BC
Bài 3: Cho ∆ABC cõn tại A và hai đường trung tuyến BM, CN cắt nhau tại K
a) Chứng minh rBNC= rCMB
b)Chứng minh ∆BKC cõn tại K
c) Chứng minh BC < 4.KM
Bài 4): Cho ∆ ABC vuụng tại A cú BD là phõn giỏc, kẻ DE ⊥ BC ( E∈BC ). Gọi F là giao điểm của AB và DE.
 Chứng minh rằng 
a) BD là trung trực của AE
b) DF = DC
c) AD < DC;
d) AE // FC.
Bài 5)Cho tam giỏc ABC vuụng tại A, gúc B cú số đo bằng 600 . Vẽ AH vuụng
gúc với BC, (H ∈ BC ) .
a. So sỏnh AB và AC; BH và HC;
b. Lấy điểm D thuộc tia đối của tia HA sao cho HD = HA. Chứng minh rằng hai tam giỏc AHC và DHC bằng nhau.
 c. Tớnh số đo của gúc BDC.
Bài 6 . Cho tam giỏc ABC cõn tại A, vẽ trung tuyến AM. Từ M kẻ ME vuụng gúc với AB tại E, kẻ MF vuụng gúc với AC tại F.
 a. Chứng minh ∆BEM= ∆CFM .
b. Chứng minh AM là trung trực của EF.
c. Từ B kẻ đường thẳng vuụng gúc với AB tại B, từ C kẻ đường thẳng vuụng gúc với AC tại C, hai đường thẳng này cắt nhau tại D. Chứng minh rằng ba điểm A, M, D thẳng hàng.
Bài 7)
Cho tam giỏc ABC cõn tại A, đường cao AH. Biết AB = 5 cm, BC = 6 cm.
a) Tớnh độ dài cỏc đoạn thẳng BH, AH?
b) Gọi G là trọng tõm tam giỏc ABC. Chứng minh rằng ba điểm A, G, H thẳng hàng. c) Chứng minh hai gúc ABG và ACG bằng nhau
Bài 8): Cho ∆ABC cú AC > AB, trung tuyến AM. Trờn tia đối của tia MA lấy
điểm D sao cho MD = MA . Nối C với D
 a. Chứng minh .Từ đú suy ra:
Kẻ đường cao AH. Gọi E là một điểm nằm giữa A và H. 
So sỏnh HC và
HB; EC và EB.
-----------------------------------
Tiết 61 – 63 ôn tập (TT)
NG: ..........................
I/ Mục tiêu:
- Giúp HS củng cố kiến thức đã học.
- Rèn kĩ năng chứng minh hình học.
II/ Tiến trình dạy học:
Bài 9)Cho ∆ABC (Â = 900) ; BD là phõn giỏc của gúc B (D∈AC). Trờn tia BC lấy điểm E sao cho BA = BE.
a) Chứng minh DE ⊥ BE.
b) Chứng minh BD là đường trung trực của AE.
 c) Kẻ AH ⊥ BC. So sỏnh EH và EC.
Bài 10): Cho tam giỏc nhọn ABC cú AB > AC, vẽ đường cao AH. a. Chứng minh HB > HC
b. So sỏnh gúc BAH và gúc CAH.
 c. Vẽ M, N sao cho AB, AC lần lượt là trung trực của cỏc đoạn thẳng HM, HN. Chứng minh tam giỏc MAN là tam giỏc cõn.
Bai 11)Cho gúc nhọn xOy, trờn 2 cạnh Ox, Oy lần lượt lấy 2 điểm A và B sao cho OA = OB, tia phõn giỏc của gúc xOy cắt AB tại I. 
a) Chứng minh OI ⊥ AB .
b) Gọi D là hỡnh chiếu của điểm A trờn Oy, C là giao điểm của AD với OI.
Chứng minh BC ⊥ Ox .
Bài 12) Cho tam giỏc ABC cú \ = 900 , AB = 8cm, AC = 6cm .
a. Tớnh BC .
b. Trờn cạnh AC lấy điểm E sao cho AE= 2cm;trờn tia đối của tia AB lấy điểm D sao cho AD=AB. Chứng minh ∆BEC = ∆DEC . 
c. Chứng minh DE đi qua trung điểm cạnh BC .
-----------------------------------
Tiết 64 – 66 ôn tập cuối năm
NG: ..........................
I/ Mục tiêu:
- Giúp HS củng cố kiến thức đã học.
- Rèn kĩ năng chứng minh hình học.
II/ Tiến trình dạy học:
Câu 1: Cho tam giác ABC có Â < 900. Vẽ ra phía ngoài tam giác đó hai đoạn thẳng AD vuông góc và bằng AB; AE vuông góc và bằng AC.
Chứng minh: DC = BE và DC BE
Gọi N là trung điểm của DE. Trên tia đối của tia NA lấy M sao cho NA = NM. Chứng minh: AB = ME và ABC = EMA 
Chứng minh: MA BC
a/ 
Xét ADC và BAF ta có:
DA = BA(gt)
AE = AC (gt)
DAC = BAE ( cùng bằng 900 + BAC )
=> DAC = BAE(c.g.c )
=> DC = BE
Xét AIE và TIC
I1 = I2 ( đđ)
E1 = C1( do DAC = BAE)
=> EAI = CTI
=> CTI = 900 => DC BE
b/ Ta có: MNE = AND (c.g.c)
=> D1 = MEN, AD = ME
mà AD = AB ( gt) 
=> AB = ME (đpcm) (1)
Vì D1 = MEN => DA//ME => DAE + AEM = 1800 ( trong cùng phía )
mà BAC + DAE = 1800
=> BAC = AEM ( 2 )
Ta lại có: AC = AE (gt) ( 3). Từ (1),(2) và (3) => ABC = EMA ( đpcm)
c/ Kéo dài MA cắt BC tại H. Từ E hạ EP MH
Xét AHC và EPA có:
CAH = AEP ( do cùng phụ với gPAE )
AE = CA ( gt)
PAE = HCA ( do ABC = EMA câu b)
=> AHC = EPA
=> EPA = AHC
=> AHC = 900
=> MA BC (đpcm)
Bài 2: 
Cho DABC vuông tại A (AB > AC ) , tia phân giác của góc B cắt AC tai D Kẻ DH vuông góc với BC , trên tia AC lấy điểm E sao cho AE = AB , đường thẳng vuông góc với AE tại E cắt tia DH ở K, chứng minh :
1
3
B
A
M
E
K
C
H
D
2
4
 a) BA = BH ; 
b) góc DBK = 450 
a)DBAD = DBHD ị BA = BH 
b) Kẻ BM ^ EKị BM = AE = AB = BH 
ịDBMK = DBHKị góc B3 = góc B4 
Mà, góc B1 = góc B2
 góc B1 + góc B2+ góc B3 + góc B4= 900
ị góc DBK = góc B2+ góc B3 = 450
Bài 3: 
Cho DABC đều , phân giác BD , CE cắt nhau tại O chứng minh rằng 
a)BD AC ; 
b) CEAB ;
A
C
B
O
D
E
c) OA =OB = OC ; 
d) Tính số đo góc AOC
a)DABD = DCBD ị góc ADB = góc CDB = 900
ịBD^AC, tương tự CE^AB
b) DOBC cân ịOB = OC
tương tự OA = OB 
ị OA = OB = OC
c)góc AOC = 1800 – 300-300 = 1200