Đề cương ôn tập cuối năm Toán 7
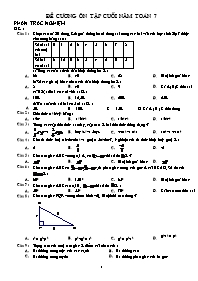
C©u 1 : Chọn câu trả lời đúng. Kết quả thống kê từ dùng sai trong các bài văn của học sinh lớp 7 được cho trong bảng sau:
Số từ sai của một bài
Số bài có từ sai
a/ Tổng các tần số của dấu hiệu thống kê là:
A. 36 B. 40 C. 28 D. Một kết quả khác
b/ Số các giá trị khác nhau của dấu hiệu thông kê là:
A. 8 B. 40 C. 9 D. Cả A; B; C đều sai
c/ Tỉ lệ số bài có 4 từ viết sai là:
A. 10% B. 12,5% C. 20% D. 25%
A
C©u 2 : d/Tần suất của số bài có 5 từ sai là:
5% B 10% C 15% D Cả A; B; C đều đúng
Đơn thức (a2b3c)2 bằng:
A. a0bc B. a4b5c2 C. a4b6c2 D. a4b6c0
Bạn đang xem tài liệu "Đề cương ôn tập cuối năm Toán 7", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
ĐỀ CƯƠNG ÔN TẬP CUỐI NĂM TOÁN 7 PHẦN TRẮC NGHIỆM ĐỀ 1 C©u 1 : Chọn câu trả lời đúng. Kết quả thống kê từ dùng sai trong các bài văn của học sinh lớp 7 được cho trong bảng sau : Số từ sai của một bài 0 1 2 3 4 5 6 7 8 Số bài có từ sai 6 12 0 6 5 4 2 0 5 a/ Tổng các tần số của dấu hiệu thống kê là : A. 36 B. 40 C. 28 D. Một kết quả khác b/ Số các giá trị khác nhau của dấu hiệu thông kê là : A. 8 B. 40 C. 9 D. Cả A; B; C đều sai c/ Tỉ lệ số bài có 4 từ viết sai là : A. 10% B. 12,5% C. 20% D. 25% A C©u 2 : d/Tần suất của số bài có 5 từ sai là : 5% B 10% C 15% D Cả A ; B ; C đều đúng Đơn thức (a2b3c)2 bằng : A. a0bc B. a4b5c2 C. a4b6c2 D. a4b6c0 C©u 3 : Trong các cặp đơn thức sau đây, cặp nào là hai đơn thức đồng dạng ? A. và B. 3xy2z4 và 5xyz C. -4xt2 và x2t D. ax3 và -4ax3 C©u 4 : Cho đa thức f(x) = 3-2x+5x2 và g(x) = 5x2+3x-7. Nghiệm của đa thức hiệu f(x)- g(x) là : A. 2 B. C. D. -2 C©u 5 : Cho tam giác ABC vuông tại A, có thì số đo là ? A. B. C. Một kết quả khác D. C©u 6 : Cho tam giác ABC có .tia phân giác trong của góc A cắt BC ở D. Số đo của là : A. 300 B. 1500 C. 650 D. Một kết quả khác C©u 7 : Cho tam giác ABC cân tại B, thì số đo là : A. 500 B. 550 C. 700 D. Cả3câu trên đều sai C©u 8 : Cho tam giác PQR vuông (theo hình vẽ). Mệnh đề nào đúng ? A. r2 = q2-p2 B. p2+q2 = r2 C. q2 = p2-r2 D. q2-r2 = p2 C©u 9 : Trọng tâm của một tam giác là điểm cắt nhau của : A. Ba đường trung trực của các cạnh B. Ba đường cao C. Ba đường trung tuyến D. Ba đường phân giác của ba góc C©u 10 : Trong tam giác MNP, điểm I được gọi là : A. Trọng tâm tam giác B. Tâm đường tròn ngoại tiếp C. Trực tâm tam giác D. Tâm đường tròn nội tiếp C©u 11 : Tìm x trên hình : x A. 2 B. 4 C. 6 D. 3 Câu 12: Điền vào chổ trống() Đồ thị của hàm số y= ax là Trực tâm của tam giác là giao điểm của ĐỀ 2 I-PHẦN TRẮC NGHIỆM A- BÀI 1 : Chọn câu trả lời mà em cho là đúng nhất. CÂU 1:.Kết quả của phép tính : -4 x2y3 .(-x) 3y2x là : a) 9x4y5. b)- 9x4y5.. c) 9x4y6. d) một kết quả khác CÂU 2: Nghiệm của đa thức P(x) = - 4x+3 là : a) . b) -. c) . d) một số khác . CÂU 3: Bậc của đa thức A= 5 x2y + 2xy - 5 x2y + 2x + 3 là : a) 3. b) 2. c) 1. d) một số khác. CÂU 4: Giá trị của biểu thức A = x2 + x -1 tại x = -là : a) 3. b) 4. d) 5. d) một số khác. CÂU 5: Đơn thức đồng dạng với 2 x2y là : a) 3xy2. b) 0 x2y . c) -4 x2y . d) khơng cĩ. CÂU 6: Nghiệm của đa thức P(x) = x2+ 4 là : a) 2. b) -2 c) -4. d) khơng cĩ. CÂU 7: Cho tam giác ABC cĩ  = 80 0 , = 700 , thì ta cĩ a) AB > AC. b) AB < AC. c) BC< AB. d) BC< AC. CÂU 8: Bộ ba số đo nào dưới đây khơng thể là chiều dài ba cạnh của một tam giác ; a) 8cm; 10 cm; 8 cm. b) 4 cm; 9 cm; 3 cm. c) 5 cm; 5 cm ; 8 cm d) 3 cm; 5 cm; 7 cm . CÂU 9: Bộ ba số đo nào dưới đây cĩ thể là chiều dài ba cạnh của một tam giác vuơng: a) 6cm; 7cm; 10 cm. b) 6cm; 7cm; 11 cm. c)6cm; 8cm; 11 cm. d)6cm; 8cm; 10 cm. CÂU 10: Cho tam giác ABC cân tại A , cĩ số đo gĩc ngồi tại B là 115 0 thì số đo gĩc  là ; a) 650. b) 130 0. c) 500. d) 90 0. CÂU 11: Cho tam giác ABC cĩ AB = 8cm . AC = 2cm , số đo BC là số nguyên chẳn thì chu vi tam giác ABC là : : a) 16cm. b) 20cm. c) 18cm. d) một số khác. CÂU 12: Cho tam giác ABC cân tại A, cĩ AB = 2,9cm và BC = 5,9 cm thì ta sẽ cĩ : a)  . CÂU 13: Cho tam giác ABC cĩ AM, BN là hai đường trung tuyến , G là giao điểm của AM và BN thì ta cĩ : a) AG = 2 GM. b) GM = AM. c)GB = BN. d) GN = GB. CÂU 14: Cho tam giác ABC cân tại A ; BC = 8cm. Đường trung tuyến AM = 3cm, thì số đo AB là : a) 4cm. b) 5cm. c) 6cm. d) 7cm. B-BÀI 2 : Thu nhập bình quân của cơng nhân xí nghiệp A được thể hiện ở biểu đồ sau ( tính bằng usd) Câu 1 : Thu nhập bình quân của cơng nhân xí nghiệp A ở năm 2004 là : a) 200usd b) 370usd c) 600usd d) một giá trị khác. Câu 2 :từ năm 2002 đến năm 2006 Thu nhập bình quân của cơng nhân xí nghiệp A tăng lên được : a) 500 usd . b) 400usd c) 300usd d) một giá trị khác. ĐỀ 3 I. Trắc nghiệm: A.Chọn chữ cái đứng trước câu trả lời đúng nhất: Câu 1:Số điểm thi môn toán của một nhóm 20 học sinh được ghi lại như sau: 8 7 9 10 7 5 8 7 9 8 6 7 6 9 10 7 9 7 8 4 a)Số các giá trị của dấu hiệu phải tìm là: A, 10 B. 7 C.20 D. Một kết quả khác b) Số các giá trị khác nhau của dấu hiệu là: A. 7 B.10 C.20 D. Một kết quả khác c) Tần số của học sinh có điểm 7 là: A.8 B.5 C.6 D. Một kết quả khác d)Điểm trung bình của nhóm học sinh trên được tính bằng số trung bình cộng là : A.7,55 B.8,25 C.7,25 D. Một kết quả khác Câu 2: Cho đa thức M = x6 + x2y3 – x5 + xy bậc của đa thức M là: A.2 B.5 C.6 D. Một kết quả khác Câu 3: Đa thức Q(x)= x2 – 4x + 3 có nghiệm là: A. -1 ; 3 B. 1; -3 C. -1 ; -3 D. 1 ; 3 Câu 4: Đơn thức nào sau đây đồng dạng với đơn thức -5x2y là: A. x2y2 B. 7 x2y C. -5 xy3 D. Một kết quả khác Câu 5: Giá trị của biểu thức M = -2x2 -5x +1 tại x = 2 là: A.-17 B.20 C.-20 D. Một kết quả khác Câu 6:Cho tam giác ABC biết góc A =600 ; góc B = 1000 .So sánh các cạnh của tam giác là: A. AC> BC > AB ; B.AB >BC >AC ; C. BC >AC AB ; D. AC >AB >BC Câu 7: Cho có AC= 1cm ,BC = 7 cm . Độ dài cạnh AB là: A. 10 cm B.7 cm C. 20 cm D. Một kết quả khác Câu 8:Cho vuông tại A. Biết AB = 8 cm , BC = 10 cm ; Số đo cạnh AC bằng: A. 6 cm B.12 cm C. 20 cm D. Một kết quả khác Câu 9: Cho cân tại A, có góc A bằng 1000. Tính góc B? A. 450 B.400 C. 500 D. Một kết quả khác B. Chọn từ đúng (Đ) hoặc sai (S). Câu 10: Trong một tam giác vuông hai góc nhọn phụ nhau. Đ S Câu 11: Nếu góc A là góc ở đỉnh của một tam giác cân thì < 900 . Đ S C. Điền vào chỗ trống (..). Câu 12: a) Một tam giác cân có độ dài hai cạnh là 3,9 cm và 7,9 cm thì chu vi của nó là:. b)Tam giác ABC có bằng 700 . I là giao điểm ba đường phân giác trong tam giác thì: =.. PHẦN TỰ LUẬN I. Đại số 1. Tính a) ; b) 2. Ba tấm vải có tổng chiều dài là 210 m. Sau khi bán tấm thứ nhất, tấm thứ hai và tấm thứ ba thì chiều dài càn lại của ba tấm vải bằng nhau. Hỏi mỗi tấm vảilúc đầu dài bao nhiêu mét? 3. Hai xe ô tô đi trên quãng đường AB dài 520 km, đi ngược chiều nhau. Tính xem hai xe gặp nhau tại điểm cách A bao nhiêu km, biết xe đi từ A đến B hết 12 giờ, xe đi từ B đến A hết 14 giờ. Lúc đó mỗi xe đã đi hết mấy giờ? 4. Chia số -910 thành bốn số, số thứ nhất và số thứ hai tỉ lệ với 2 và 3, số thứ hai và ba tỉ lệ với 4 và 5, số thứ ba và tư tỉ lệ với 5 và 7. 5. Cho hàm số y=f(x) được xác định bởi công thức . a) Hãy tìm các giá trị của x để vế phải của công thức có nghĩa. b) Tìm f(-2); f(-1); f(0); f(1); f(2). c) Xác định hoành độ của điểm A thuộc đồ thị hàm số trên biết tung độ A là -1. d) Xác định tung độ điểm B thuộc đồ thị hàm số trên biết hoành độ của B là -. 6. Kết quả điều tra điểm thi môn toán của khối 7 của một trường THCS được một bạn học sinh ghi lại dưới bảng sau. 9 2 7 8 10 6 5 4 3 5 8 9 5 7 7 6 7 1 1 7 4 7 4 10 8 10 8 7 8 4 7 8 7 8 7 2 2 9 6 8 5 7 8 9 8 9 8 5 3 10 5 9 9 8 9 5 9 6 9 6 6 8 9 4 6 9 6 6 6 5 5 8 9 7 4 5 4 5 5 3 5 4 6 7 7 6 10 6 5 6 4 4 7 2 8 5 4 5 5 7 2 4 8 5 8 3 9 6 5 3 8 9 3 10 7 1 9 1 7 9 a) Dấu hiệu cần tìm hiểu ở đâu là gì? b) Số các giá trị là bao nhiêu, số các giá trị khác nhau là mấy? c) Lập bảng tần số. d) Tính ; tìm M0, nhận xét. e) Vễ đồ thị đoạn thẳng biểu thị. 7. Thu gọn các đơn thức sau rồi cho biết phần hệ số, biến, tìm bậc. c) d) a) b) 8. Tính giá trị của: a) 15x4+ 7x4 +(-20x2).x2 tại x= -1. b) 23x3y3+ 17x3y3+(-50x3).y3 tại x=1, y= -1. 9. Cho . a) Thu gọn M. b) Với giá trị nào của a thì M không âm với mọi x, y? c) Với giá trị nào của a thì M không dương với mọi x, y? d) Cho a=2. Tìm các cặp số nguyên (x; y) để M= 84. 10. Cho A= 2x2 - 5xy + 3y2; B= 3x2 + 2xy + y2; C= -x2 + 3xy + 2y2.Tính A + B + C; B – C - A; C – A – B. 11. Cho đa thức f(x) = 3x-6. Tìøm các giá trị của biến sao cho: a) f(x) = 0; b) f(x) = 1; c) f(x) > 0; d) f(x) < 0 12*. Tìm x biết a) |x+2|= 3; b) |x|+|x+2|= 3; c) |3x-5|= |x+2| 13*. Tìm các số nguyên x, y để a) |x-1|+|x-2| đạt giá trị nhỏ nhất; b) 10- 3|x-5| đạt giá trị lớn nhất; c) -15-|2x-4|-|3y+9| đạt giá trị lớn nhất; d) là một số nguyên; 14. Biết đồ thị hàm số y=f(x)= 2x+5 và y=f(x)= x+3 cắt nhau tại điểm M. Tìm toạ độ điểm M. 15*. Tính giá trị biểu thức A= 3x2- 3xy +2y2 với |x|=1, |y|=3. B= tại x= -4, y= 16, z= -5 II. Hình học 1. Bài 1. Cho đoạn thẳng AB, điểm C và D cách đều hai điểm A, B và khác phía đối với AB. CD cắt AB tại I. Chứng minh : CD là tia phân giác của gĩc ACB CD là đường trung trực của AB Kết quả trên cịn đúng khơng nếu C, D cùng phía AB HD: a) rACD = rBCD ( c.c.c) ; b) rACI = rBCI (c.g.c) c) I1 = I2 = 900 và IA = IB 2. Bài 2. Cho gĩc xOy. Trên Ox lấy điểm A, trên Oy lấy B sao cho OA = OB. Lấy M, N đều thuộc miền trong của gĩc sao cho MA = MB, NA = NB. Chứng minh : OM là phân giác gĩc xOy (rOMA = rOMB ) O, M, N thẳng hàng ( OM, ON cùng là pg gĩc xOy ), MN là đường trung trực của AB. 3. Bài 3. Cho tam giác ABC cĩ . Gọi M và N lần lượt là trung điểm của AC và AB. Trên tia đối của tia MB lấy K sao cho MK = MB. Trên tia đối của tia NC lấy I sao cho NI = NC. Tính Chứng minh IB//AC, AK//BC Chứng minh A là trung điểm của IK 4. Bài 4. Cho gĩc xOy. Trên tia Ox lấy M, N. Trên tia Oy lấy P, Q sao cho OM = OP, PQ = MN. Chứng minh : (HD : c.g.c) (HD : c.c.c) c. Gọi I là giao điểm của MQ và PN. Chứng minh (HD : g.c.g) Chứng minh OI là tia phân giác của gĩc xOy OI là tia đường trung trực của MP f. MP//NQ (HD : cùng vuơng gĩc với OI ). 5. Bài 5. Cho tam giác ABC vuơng tại A. Kẻ . Kẻ HP vuơng gĩc với AB và kéo dài để cĩ PE = PH. Kẻ HQ vuơng gĩc với AC và kéo dài để cĩ QF = QH Chứng minh Chứng minh E, A, F thẳng hàng và A là trung điểm của EF Chứng minh BE//CF Cho AH = 3cm, AC = 4cm. Tính HC, EF 6. Bài 6. Cho tam giác ABC. Kẻ AH vuơng gĩc với BC. Trên tia đối của tia AH lấy D sao cho AH = AD. Lấy trung điểm E của HC. Gọi F là giao điểm của AC và DE. Chứng minh : AF = 1/3AC H, F và trung điểm M của DC thẳng hàng HF = 1/3DC 7. Bài 1. Cho tam giác ABC vuơng tại A. Trung tuyến AM. Trên tia đối tia MA lấy D sao cho MD = MA. Chứng minh vuơng Gọi K là trung điểm AC. Chứng minh KB = KD Gọi I là giao điểm của KD và BC, N là giao điểm của KB và AD. Chứng minh tam giác KNI cân d. Chứng minh . Điều này cịn đúng khơng nếu tam giác ABC khơng là tam giác vuơng. 8. Bài 8. Cho tam giác ABC cĩ AB = 9cm, AC = 12cm, BC = 15cm Tam giác ABC là tam giác gì ? Vẽ trung tuyến AM. Kẻ . Trên tia đối của tia MH lấy K sao cho MK = MH Chứng minh . Suy ra BK//AC BH cắt AM tại G. Chứng minh G là trọng tâm của tam giác ABC Tính độ dài AG. 9. Bài 9. Cho cĩ . Các phân giác AD và CE gặp nhau ở O. Đường thẳng chứa tia phân giác ngồi tại đỉnh B của tam giác ABC cắt đường thẳng AC tại F. Chứng minh : a. b. c. Ba điểm D, E, F thẳng hàng. 10. Bài 10. Cho tam giác ABC cân tại A. trên hai cạnh AB, AC và về phía ngồi tam giác vẽ các tam giác đều ADB, AEC Chứng minh BE =CD Kẻ phân giác AH của tam giác cân. Chứng minh BE, CD, AH đồng quy. 11. Bài 11. Cho tam giác ABC. Trung tuyến AD, BE, CF. Chứng minh : a. b. 12. Bài 12. Cho tam giác ABC vuơng tại A. Đường phân giác BE. Kẻ EH vuơng gĩc với BC. Gọi K là giao điểm của AB và HE. Chứng minh : a. b. BE là đường trung trực của AH c. EK = EC d. AE < EC e. f. Cho AB = 3cm, BC = 5cm. Tính KC 13. Bài 13. Cho gĩc vuơng xOy, điểm A thộc tia Ox, B thuộc Oy. Đường trung trực của OA cắt Ox tại D, đường trung trực của OB cắt Oy ở E. Gọi C là giao điểm của hai đường trung trực đĩ. Chứng minh : CE = OD CE vuơng gĩc với CD CA = CB CA//DE A, B, C thẳng hàng. 14. Bài 14. Cho tam giác DEF cân tại D cĩ DE = DF = 5cm, EF = 8cm. M, N lần lượt là trung điểm DF và DE. Kẻ . Chứng minh EM = FN và Giao điểm của EM và FN là K. Chứng minh KE = KF Chứng minh DK là phân giác của gĩc EDF Chứng minh EM, FN, AH đồng quy Tính AH 15 Bài 15. Cho tam giác ABC, trung tuyến AM. Trên AM lấy I, K sao cho AI = IK = KM. Gọi N, P lần lượt là trung điểm của AC và AB Chỉ ra các điểm thẳng hàng D là giao điểm của BN và CI thì D là trọng tâm của tam giác nào ? Cho BN = 18cm. Tính DN 16. Bài 16. Cho tam giác ABC vuơng tại A, đường trung trực của AB cắt AB tại E và BC tại F Chứng minh FA = FB Vẽ , chứng minh Chứng minh FH = AE Chứng minh EH//BC và EH = ½ BC. 17. Bài 17. Cho tam giác ABC vuơng ở C cĩ . Tia phân giác của gĩc BAC cắt BC ở E. Kẻ . Chứng minh : AC = AK và AE vuơng gĩc với CK KA = KB EB > AC AC, BD, KE cùng đi qua một điểm Bµi 18. Cho tam gi¸c ABC vu«ng ë A, cã AB = 5cm, BC = 13cm. Ba ®êng trung tuyÕn AM, BN, CE c¾t nhau t¹i O. TÝnh AM, BN, CE. b. TÝnh diƯn tÝch tam gi¸c BOC Bµi 19.Cho tam gi¸c ®Ịu AOB, trªn tia ®èi cđa tia OA, OB lÊy theo thø tù c¸c ®iĨm C vµ D sao cho OC = OD.Tõ B kỴ BM vu«ng gãc víi AC, CN vu«ng gãc víi BD. Gäi P lµ trung ®iĨm cđa BC.Chøng minh: a.Tam gi¸c COD lµ tam gi¸c ®Ịu b.AD = BC c.Tam gi¸c MNP lµ tam gi¸c ®Ịu Bµi 20. Cho tam gi¸c c©n ABC, AB = AC, ®êng cao AH. KỴ HE vu«ng gãc víi AC. Gäi O lµ trung ®iĨm cđa EH, I lµ trung ®iĨm cđa EC. Chøng minh: IO vu«ng gãc v¬i AH b. AO vu«ng gãc víi BE Bµi 21.Cho tam gi¸c nhän ABC. VỊ phÝa ngoµi cđa tam gi¸c vÏ c¸c tam gi¸c vu«ng c©n ABE vµ ACF ë B vµ C.Trªn tia ®èi cđa tia AH lÊy ®iĨm I sao cho AI = BC. Chøng minh: Tam gi¸c ABI b»ng tam gi¸c BEC BI = CE vµ BI vu«ng gãc víi CE. Ba ®êng th¼ng AH, CE, BF c¾t nhau t¹i mét ®iĨm bbbbbbbbbbENDbbbbbbbbbb
Tài liệu đính kèm:
 On tap toan 7Hoc ki II.doc
On tap toan 7Hoc ki II.doc





