Đề cương ôn tập Toán 7 - Học kỳ II - Đại số
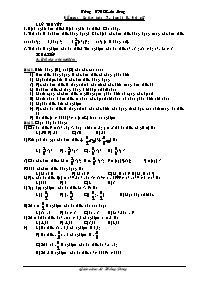
Bài 1. Điền đúng (Đ), sai (S) cho các câu sau:
1) Đơn thức đồng dạng là các đơn thức có cùng phần biến
2) Mọi số thực đều là các đơn thức đồng dạng
3) Bậc của đơn thức là tổng số mũ của tất cả các biến trong đơn thức đó
4) Hai đơn thức có tổng bằng 0 khi hệ số đối nhau
5) Muốn cộng các đơn thức ta giữ nguyên phần biến và cộng các hệ số
6) Muốn nhân 2 đơn thức ta nhân các hệ số với nhau và nhân phần biến với nhau
7) Mọi đa thức đều có nghiệm
8) Bậc của đa thức là tổng số mũ của các biến của hạng tử có bậc cao nhất trong đa thức đó
Bạn đang xem tài liệu "Đề cương ôn tập Toán 7 - Học kỳ II - Đại số", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Đề cương ôn tập toán 7 - học kỳ II - Đại số
I. Lý thuyết
1. Định nghĩa đơn thức? Định nghĩa đa thức? Cho ví dụ.
2. Thế nào là hai đơn thức đồng dạng? Xác định các đơn thức đồng dạng trong các đơn thức sau: 5x2y; 0,25xy2; 1(x2y)2; ax2y (a là hằng số).
3. Thế nào là nghiệm của đa thức? Tìm nghiệm của đa thức x2 - 3 ; -3x + 5; x2 - 4x + 3
II. Bài tập
A. Bài tập trắc nghiệm
Bài 1. Điền đúng (Đ), sai (S) cho các câu sau:
Đơn thức đồng dạng là các đơn thức có cùng phần biến
Mọi số thực đều là các đơn thức đồng dạng
Bậc của đơn thức là tổng số mũ của tất cả các biến trong đơn thức đó
Hai đơn thức có tổng bằng 0 khi hệ số đối nhau
Muốn cộng các đơn thức ta giữ nguyên phần biến và cộng các hệ số
Muốn nhân 2 đơn thức ta nhân các hệ số với nhau và nhân phần biến với nhau
Mọi đa thức đều có nghiệm
Bậc của đa thức là tổng số mũ của các biến của hạng tử có bậc cao nhất trong đa thức đó
Đa thức (x + 1000)2 + a (aR) luôn vô nghiệm
Bài 2. Chọn đáp án đúng:
1) Cho đa thức P = 3x2 - 2y3 - 5xy với x = -2; y = -3 thì đa thức có giá trị là:
A) -96 B) -72 C) 36 D) -12
2) Kết quả thu gọn của đơn thức -(-)2.(-) là:
A) x3y2 B) -x5y3 C) -x3y2 D) x5y3
3) Cho các đơn thức: M = x3y2; N =-x2y3; P = (xy)2(-3x); Q = (xy)3
Khi đó các đơn thức đồng dạng là:
A) M và N B) M và P C) M, N và P D) M, N và Q
4) Bậc của đa thức f(x) = x100 -2x5 - 2x3 + 3x4 + x - 1999 + x5 - x100 + 1 + x5 là:
A) 100 B) 5 C) 4 D) 3
5) Tập hợp nghiệm của đa thức 4x3 - 9x là:
A) {} B) {-} C){ ; -} D) Một đáp số khác
6) Số x = là nghiệm của đa thức nào sau đây:
A) 3x - 2 B) 2x + 3 C) 2x - 3 D) 4x2 -12x - 9
7) Số m để đa thức 2x2 - mx + 0,5 có nghiệm x = -2 là:
A) -4,75 B) -4,25 C) 3,75 D) 4,25
8) A) Đa thức 3x - 0,5 có nghiệm là 1,5;
B) Đa thức -x - 1 có nghiệm là -
C) Số 1 và - là nghiệm của đa thức 2x2 -x - 1;
D) Số -1 là nghiệm của đa thức x2 + 2009x + 2010
B. Bài tập tự luận
Bài 1. Thu gọn các đơn thức sau rôi tìm hệ số, bậc của đơn thức
-4,9(xa)4(y)2(-x2y)5 với a là hằng số;
với b là hằng số
Bài 2. Cho hai đa thức:
A = 2(-3x2y)2 + 5(x2y2)x2 + 2xy -7(4xy -1) + 5(x-1)
B = 2(x-1) - (-3x4y2 + 5x) - (2x + 1)y + (y - 3)
a) Thu gọn và tính bậc của A, B; b) Tính A + B; A - B;
c) Tính C = A - 13B; d) Tính giá trị của C khi x = -1,5; y =
Bài 3. Cho hai đa thức:
C = 7x - x2y2 + 2xy - 3x2y + 4xy - 5 - 3x2y2 + x2y
D = 2xy + 3 - 8xy + 4x - 3(xy)2 + 5x2y + 3x + 1
a) Thu gọn C, D và tìm bậc; b) Tính E = 3C + 2D
c) Tìm giá trị của E khi = 0 và 2x - y = 7
Bài 4. Cho hai đa thức P(x) = x3 - x2 + x + 1; Q(x) = x3 + 2x2 - x + 2
Tính P(x) + Q(x); P(x) - Q(x)
Tính giá trị của P(x) + Q(x) khi x = 2
Bài 5. Cho hai đa thức M(x) = 2x(x - 3) - 5(x - 2) + 3x3
N(x) = -x(x + 1) - (3x - 4) + x2(2x - 3)
Thu gọn M(x); N(x)
B) Tìm nghiệm của đa thức M(x) - N(x) - x2(x + 6)
Bài 6. Cho hai đa thức
A(x) = 5x3 - (x + 3) - (4x - 1)(4x + 1);
B(x) = x2(3x - 15) + x - 10
Thu gọn A(x); B(x); b) Tính C(x) = A(x) - B(x) và cho biết bậc của C(x)
c) Tìm giá trị lớn nhất của đa thức P(x) = C(x) - 2x3
Bài 7. Hãy tìm nghiệm của các đa thức sau:
a) 5 - 4x b) x3 - 4x c) x3 - 2x2 + x
d) 4x2 + 5 e) -x4 - x2 - 3 f) x2 - 7x + 12
g) x(1 + 4x) - (4x2 - 3x + 1) h) x3 - x2 + 1 - x i) x2 - x + 1
Bài 8. Cho hai đa thức: P(x) = 3mx2 + 6mx + m2 - 3
Q(x) = x3 - (m + 1)x2 - 2mx + m2 - 1
Tìm m để P(-2) = Q(1)
Khi m = 1 tính giá trị của P(x) + Q(x) với = 1
Bài 9. Xác định hệ số a, b, c, của các đa thức:
a) M(x) = ax2 + bx + 6 biết M(x) có hai nghiệm là 1 và -2
b) P(x) = ax2 + bx + c biết P(0) = -1; P(1) = 3; P(2) = 1
Bài 10. Tìm giá trị lớn nhất, giá trị nhỏ nhất (nếu có):
a) 3x2 - 2x + 5 b)9 - 5x - x2 c) -x2 -4y2 - z2 + 2x - 6y + 10z + 1975
Đề cương ôn tập toán 7 - học kỳ II - hình học
Đề cương ôn tập học kì II môn hình học
Phần I: Lý thuyết
Câu 1: Nêu các trường hợp bằng nhau của tam giác? Vẽ hình minh hoạ?
Câu 2: Nêu định lí Pitago (Định lý thuận, định lý đảo)
áp dụng tính: Cho tam giác ABC vuông tại A có AB = 8, BC = 10 cm. Tính AC.
Câu 3: Nêu định nghĩ, tính chất tam giác cân, tam giác đều.
Nêu các cách chứng minh một tam giác là tam giác cân, tam giác đều?
Câu 4: Nêu định lý về quan hệ giữa đường xiên và đường vuông góc, đường xiên và hình chiếu.
Câu 5: Nêu bất đẳng thức tam giác.
Câu 6: Nêu tính chất về ba đường trung tuyến, ba đường phân giác, ba đường cao, ba đường trung trực của tam giác.
Phần II: Bài tập
Bài 1: Cho ABC vuông tại A có BF là đường phân giác của góc B, H là hình chiếu của C trên BF. Trên tia đối của tia HB lấy điểm E sao cho HE = HF, K là hình chiếu của F trên BC. Chứng minh rằng:
a) CFE cân, AK//HC; b) So sánh FA và FC;
c) EBC vuông; d) các đường thẳng CH, FK và AB đồng quy.
Bài 2: Cho ABC vuông tại A (AB < AC) I là trung điểm của BC, đường trung trực của BC cắt AC tại E, D thuộc tia đối của AC sao cho AD = AE. Nối BE. CMR
a) = 2;
b) BD giao với AI tại M chứng minh rằng MD = AD, MB = AC
c) DE < BC;
d) Gọi EI giao với BA tại K, cmr: BE KC;
e) Tìm điều kiện của ABC để AI BE
Bài 3: Cho ABC trung tuyến BE và CD. I thuộc tia đối của tia EB sao cho EI =BE, K thuộc tia đối của tia DC sao cho DC = DK.
Chứng minh rằng: A là trung điểm của KI;
BK giao với CI tại F, cmr: BI, CK và FI đồng quy.
Gọi giao điểm của FA và BC là P, cmr: GP = GI.
Bài 4: Cho xOy = 1v, lấy AOx, B Oy. Vẽ ABC vuông cân tại B, kẻ CH Oy.
Chứng minh rằng: OA + HC = OH;
Gọi M là trung điểm của AC, cmr: OMA = HBM;
Cmr: OMH vuông cân, Om là tia phân giác của xOy;
Bài 5: Cho ABC cân có >900,hai điểm B và E BC sao cho BD = DE = EC, kẻ BH AD, CK AE ( H AD, K AE), BH giao với CK tại G.
CMR: BH = CK;
M là trung điểm của BC và A, M, G thẳng hàng;
AC > AD;
DAE > DAB.
Bài 6: Cho ABC có ba góc nhọn, đường cao AH, vẽ ra phía ngoài của ABC các tam giác vuông cân ABE (tại B) và ACF (tại C). trên tia đối của tia AH lấy M sao cho AM = BC. Cmr
a) ABM = BEC;
b) BM CE, CM BF;
c) Các đường thẳng AH, CE và BF cắt nhau tại một điểm.
d) ABC có điều kiện gì để A là trung điểm của EF.
Bài 7: Cho ABC vuông tại A, (AB < AC, đường cao AH). AD là tia phân giác của AHC, kẻ DE AC tại E. Cmr
a) BAD cân;
b) Gọi K là giao điểm của DE và AH. Cmr HDK = EDC;
c) HE // KC;
d) Tam giác ABC có điều kiện gì để H là trung điểm của AK. Khi đó chứng minh HPE đều, biết AD giao với KC tại P.
e) Biết BH = 18cm, CH = 32cm, tính AC?
Bài 8: Cho ABC vuông cân tại A, hai tia phân giác BE và CF, kẻ EH BC tại H.
Cmr: BE là trung trực của AH;
AF = EH;
Kẻ FK // AH (K BC) Cmr: H là điểm của KC;
Gọi KF giao với BE tại I, Cmr I là trung điểm của BE và AHI vuông cân;
Gọi BE giao với CF tại O; Cmr HO//AC.
Bài 9: Cho ABC có ba góc nhọn, đường cao AD, xác định M và N sao cho AB là trung trực của DM và AC là trung trực của DN. MN giao với AB và AC thứ tự tại I và K. Cmr:
a) MAsN = 2 BAC;
b) ANM cân, BMA vuông
c) DA là phân giác của IDK;
d) BK AC, CI AB.
Tài liệu đính kèm:
 De cuong on tap nam hoc ki II.doc
De cuong on tap nam hoc ki II.doc





