Đề kiểm tra chương 1 môn Hình học lớp 8 (đề số 2)
I. Trắc nghiệm khách quan
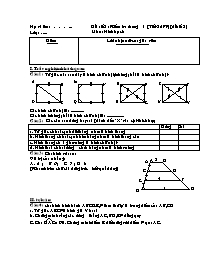
Câu 1: Tứ giác nào sau đây là hình chữ nhật; không phải là hình chữ nhật
Các hình chữ nhật là: .
Các hình không phải là hình chữ nhật là: .
Câu 2: Các câu sau đúng hay sai ( đánh dấu “X” vào cột thích hợp
Đúng Sai
a. Tứ giác có hai cạnh đối bằng nhau là hình thang
b. Hình thang có hai cạnh bên bằng nhau là hình thang cân
c. Hình thang có 1 góc vuông là hình chữ nhật
d. Hình thoi có hai đường chéo bằng nhau là hình vuông
Bạn đang xem tài liệu "Đề kiểm tra chương 1 môn Hình học lớp 8 (đề số 2)", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Họ và tên: .. Đề số 2 : Kiểm tra chương I (Tiết 25 PP) (đề số 2) Lớp:.... Môn: Hình học 8 Điểm Lời nhận xét của giáo viên I. Trắc nghiệm khách quan Câu 1: Tứ giác nào sau đây là hình chữ nhật; không phải là hình chữ nhật S T V U A B C D M N P Q E F G H Các hình chữ nhật là: ............. Các hình không phải là hình chữ nhật là: ................. Câu 2: Các câu sau đúng hay sai ( đánh dấu “X” vào cột thích hợp Đúng Sai a. Tứ giác có hai cạnh đối bằng nhau là hình thang b. Hình thang có hai cạnh bên bằng nhau là hình thang cân c. Hình thang có 1 góc vuông là hình chữ nhật d. Hình thoi có hai đường chéo bằng nhau là hình vuông = = = _ _ _ x 4 2 G E C A F D B Câu 3: Cho hình vẽ sau: Giá trị của x bằng: A. 5 ; B 6 ; C 7 ; D 8 (Khoanh tròn chữ cái đứng trước kết quả đúng) H II. tự luận: Câu 4: cho hình bình hành ABCD. E,F theo thứ tự là trung điểm của AB, CD a. Tứ giác AECF là hình gì ? Vì sao? b. Chứng minh rằng các đường thẳng AC, BD, EF đồng quy C. Cho DAC = 900. Chúng minh điểm E đối xứng với điểm F qua AC. Đáp án và thang điểm (đề số 2) I. trắc nghiệm khách quan : 5 điểm Câu 1: ( 2 điểm ) Ghi đúng mỗi hình cho 0,5 điểm Các hình chữ nhật là: MNPQ, EFGH Các hình không phải hình chữ nhật là: ABCD, STVU Câu 2: ( 2 điểm ) đúng mỗi ý cho 0,5 điểm Các ý a b c d Đúng x Sai x x x Câu 3:( 1 điểm ) A. 5 II. Tự luận A D C E F O Câu 4: ( 5 điểm) B - Vẽ hình đúng cho 0,5 điểm - Ghi GT, KL đúng cho 0,5 điểm GT: ABCD,AB // CD, AD // BC EAB, AE = EB FDC, FD = FC KL: a. AECF là hình gì ? vì sao b. AC, BD, EF đồng quy c. Khi DAC = 900, điểm E đối xứng với điểm F qua AC a. HS chứng minh được AECF là hình bình hành cho 1,5 điểm Học sinh có thể chứng minh: AE = 1/2 AB (gt) FC = 1/2 DC (gt) => AE = FC (1) AB = DC (gt) Vì AB // DC => AE // FC (2) Từ (1) và (2) =>AECF là hình bình hành. b. Gọi O = ACBD. Vì AC và BD là hai đường chéo của hình bình hành ABCD nên O là trung điểm cảu AC và BD Ta có tiếp AECF là hình bình hành (chứng minh câu a) có đường chéo AC và EF suy ra O là trung điểm của EF. Vậy AC, BD, EF đều cắt nhau tại điểm O (điều phải chứng minh) (HS chứng minh được như trên cho 1,5 điểm) c. Khi DAC = 900 suy ra vuông tại A, AF là đường trung tuyến ứng với cạnh huyền DC suy ra AF = DC = FC Hình bình hành AECF có hai cạnh bên AF = FC nên là hình thoi => AE = AF, CE = CF => AC là đường trung trực của đoạn thẳng EF => E đối xứng với F qua AC (câu c làm đúng cho 1 điểm) Lưu ý: - HS giải theo cách khác đúng cũng cho điểm tối đa - Điểm mỗi mục ở trên là điểm tối đa, tuỳ mức độ HS làm như thế nào mà trừ điểm cho phù hợp.
Tài liệu đính kèm:
 Hinh L8 C102.doc
Hinh L8 C102.doc





