Đề kiểm tra Chương II môn Hình học Lớp 7 (Có đáp án)

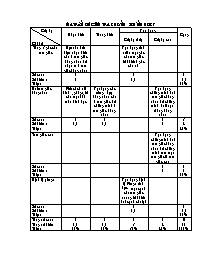
Ma trËn ®Ò kiÓm tra ch­¬ng II h×nh häc 7
 CÊp ®é
Chñ ®Ò
NhËn biÕt 
Th«ng hiÓu
VËn dông
Céng
CÊp ®é thÊp
CÊp ®é cao
Tæng 3 gãc cña tam gi¸c
Dùa vµo ®Êu hiÖu nhËn biÕt cña 2 tam gi¸c b»ng nhau ®Ó nhËn ra 2 t©m gi¸c b»ng nhau
VËn dông tÝnh sè ®o mét gãc cña tam gi¸c khi biÕt 2 gãc cña nã
Sè c©u : 
Sè ®iÓm :
TØ lÖ : 
1
1
1
1,5
2
2,5
25%
Hai tam gi¸c b»ng nhau
BiÕt c¸ch vÏ h×nh , ghi gt, kl cña mét bµi to¸n h×nh häc
VËn dông c¸c tr­êng hîp b»ng nhau cña 2 tam gi¸c ®Ó chøng minh 2 tam gi¸c b»ng nhau
VËn dông chøng minh hai tam gi¸c b»ng nhau ®Ó chøng minh hai ®o¹n th¼ng b»ng nhau
Sè c©u : 
Sè ®iÓm :
TØ lÖ : 
1
0,5
1
1,5
1
2
3
4
40%
Tam gi¸c c©n
VËn dông chøngminh hai tam gi¸c b»ng nhau ®Ó chøng minh tam mét tam gi¸c lµ tam gi¸c c©n
Sè c©u : 
Sè ®iÓm :
TØ lÖ : 
1
2
1
2
20%
§Þnh lý pitago
VËn dông ®Þnh lý Pitago tÝnh ®­îc mét c¹nh cña tam gi¸c vu«ng khi biÕt hai c¹nh cßn l¹i
Sè c©u : 
Sè ®iÓm :
TØ lÖ : 
1
1,5
1
1,5
15%
Tæng sè c©u : 
Tæng sè ®iÓm 
TØ lÖ :
2
1,5
15%
1
1,5
15%
2
3
30%
2
4
40%
6
10
100%
ĐỀ KIỂM TRA CHƯƠNG II
Môn : Hình học - Thời gian làm bài : 45 phút
HỌ TÊN:	
ĐIỂM
LỜI PHÊ CỦA THẦY
 Câu 1: (4đ)
	Cho D ABC và D A'B'C' có : ; AB = 3cm ; A'B' = 3cm 
 AC = 4cm ; A'C' = 4cm
	a, Hãy so sánh D ABC và D A'B'C'
	b, Cho = 530 ; = 600 . Tính 
	c, Giả sử = 900 . Tính BC
Câu 2 : (6đ)
	Cho tam giác ABC cân tại A . Trên tia đối của BC lấy điểm M, trên tia đối của CB lấy 	điểm N sao cho BM = CN.
 	a, Chứng minh : D ABM = D ACN
	b, Kẻ BH ^ AM ; CK ^ AN ( H AM; K AN ) . Chứng minh : AH = AK
	c, Gọi O là giao điểm của HB và KC . Tam giác OBC là tam giác gì ? Vì sao?
BÀI LÀM
HƯỚNG DẪN CHẤM ĐỀ KIẺM TRA CHƯƠNG II 
Môn : Hình học Lớp 7
Câu 
Nội dung
Điểm 
Câu1
a, Ta thấy : D ABC và D A'B'C' có hai cặp cạnh xen giữa một cặp góc tương ứng bằng nhau : 
Nên : D ABC = D A'B'C' ( c.g.c)
b, Theo câu (a) ta có : D ABC = D A'B'C'
 = 
Trong D ABC ta có tổng ba góc ( A + B + C ) = 1800 
 = 1800 - (530+ 600 )
	 = 670	
c, Nếu góc A = 900 thì D ABC vuông tại A 
 Áp dụng định lý Pitago ta có : BC2 = AB2 + AC2 
 BC2 = 32 + 42 = 25
 BC = 5 (cm) 
0,5
0,5
0,5
0,5
0,5
0,5
0,5
0,5
Câu 2
A
K
N
C
B
H
M
 D ABC, AB=AC, (MBC, NCB)
GT BM=CN; BH ^AM, CK ^ AN
 ( HAM, K AN )
KL a, D ABM = D ACN
 b, AH = AK
 c, Tam giác OBC là tam giác gì 
a, Theo (gt) D ABC cân tại A 
 = 
Mà : + = +
 = (1)
Xét : D ABM và D ACN
 Có : AB = AC (gt)
 ABM = ACN ( theo (1) )
 BM = CN ( gt )
 D ABM = D ACN ( c.g.c ) (2)
b, Xét : D ABH = D ACK là hai tam giác vuông 
 Có : Cạnh huyền : AB=AC (gt)
 Góc nhọn BAH = CAH ( từ (2) suy ra )
 D ABH = D ACK ( cạnh huyền - góc nhọn )
 AH = AK
c, Chứng minh được : D BMH = D CNK 
 = 
 = 
 D OBC cân tại O	
0,5
0,5
0,5
0,5
0,5
0,5
0,5
0,5
0,5
0,5
0,5
0,5