Đề kiểm tra học kỳ II môn Toán Lớp 7 - Năm 2011-2012 - Phòng GD & ĐT Chơn Thành (Có đáp án)

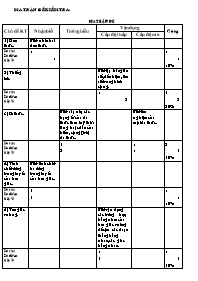
Ma trËn ®Ò kiÓm tra:
ma trËn ®Ò
Chủ đề KT
Nhận biết
Thông hiểu
Vận dụng
 Céng
Cấp độ thấp
Cấp độ cao
1) §¬n thøc.
BiÕt nh©n hai ®¬n thøc
Sè c©u
Sè ®iÓm
tØ lÖ %
1
 1
1 
 1
10%
2) Thèng kª.
BiÕt lËp b¶ng tÇn sè, dÊu hiÖu, t×m sè trung b×nh céng.
Sè c©u
Sè ®iÓm
tØ lÖ %
1
 2
1
 2
20%
3)§a thøc.
BiÕt s¾p xÕp c¸c h¹ng tö cña ®a thøc theo luü thõa t¨ng hoÆc dÇn cña biÕn, céng (trõ) ®a thøc.
BiÕt t×m nghiÖm cña mét ®a thøc.
Sè c©u
Sè ®iÓm
tØ lÖ %
1
2
1
1
2
 3
30%
4) TÝnh chÊt ®­êng trung tuyÕn cña tam gi¸c.
BiÕt tÝnh chÊt ba ®­êng trung tuyÕn cña tam gi¸c.
Sè c©u
Sè ®iÓm
tØ lÖ %
1
1
1
 1
10%
5)Tam gi¸c vu«ng.
BiÕt vËn dông c¸c tr­êng hîp b»ng nhau cña tam gi¸c vu«ng ®Ó c/m c¸c ®o¹n th¼ng b»ng nhau, c¸c gãc b»ng nhau.
Sè c©u
Sè ®iÓm
tØ lÖ %
1
3
1
 3
30%
Tổng số câu
Tổng số điểm 
Tỉ lệ % 
2
2 
20%
 1 
2 
20%
2
5
 50%
 1 
1 
 10%
6
10 100%
IV. Néi dung ®Ò kiÓm tra:
§Ò tham kh¶o
Phßng gd-®t ch¬n thµnh
kiÓm tra häc kú ii m«n to¸n 7
N¨m häc: 2011 – 2012
Thêi gian: 90 phót (kh«ng kÓ thêi gian ph¸t ®Ò)
A. Lý thuyết: (2 điểm)
Câu1: (1 điểm)
a. Để nhân hai đơn thức ta làm như thế nào? 
b. Áp dụng: Tính tích của 9x2yz và –2xy3
Câu 2: (1 điểm)
a. Nêu định lý về tính chất ba đường trung tuyến của tam giác.
b. Áp dụng: AM là đường trung tuyến xuất phát từ A của rABC, G là trọng tâm. 
 Tính AG biết AM = 9cm.
B. Bài tập: (8 điểm)
Bài 1: (2 điểm) 
Số cân nặng của 30 bạn (tính tròn đến kg) trong một lớp được ghi lại như sau:
32 36 30 32 32 36 28 30 31 28
30 28 32 36 45 30 31 30 36 32
32 30 32 31 45 30 31 31 32 31
a. Dấu hiệu ở đây là gì?
b. Lập bảng “tần số”. 
c. Tính số trung bình cộng.
Bài 2: (2 điểm)
	Cho hai đa thức:
	P() = ; Q() = 
	a. Sắp xếp các hạng tử của mỗi đa thức trên theo luỹ thừa giảm của biến.
	 b. Tính P() + Q() và P() – Q().
Bài 3: (1 điểm) 
	Tìm hệ số a của đa thức M() = a + 5 – 3, biết rằng đa thức này có một nghiệm là .
Bài 4: (3 điểm)
	Cho vuông tại A, đường phân giác BE. Kẻ EH vuông góc với BC (H BC). Gọi K là giao điểm của AB và HE. Chứng minh rằng: 
	 a) = . 
	b) BE là đường trung trực của đoạn thẳng AH.
	c) EK = EC.
	 d) AE < EC.
v. h¦íNG DÉN CHÊM, BIÓU §IÓM:
C©u
H­íng dÉn chÊm
biÓu ®iÓm
C©u 1.
a. Nêu đúng cách nhân hai đơn thức. 
b. (9x2yz).(–2xy3) = –18x3y4z 
(0,5đ)
(0,5đ)
C©u 2.
 a. Định lý: Sgk/66 
 b. 
(0,5đ)
(0,5đ)
C©u 3.
a. Dấu hiệu: Số cân nặng của mỗi bạn. 
b. Bảng “tần số”: 
Số cân (x)
28
30
31
32
36
45
Tần số (n)
3
7
6
8
4
2
N =30
c. Số trung bình cộng: 
(kg) 
(0,25 điểm)
(0,75 điểm)
(1 điểm)
C©u 4.
a) Sắp xếp đúng: P() = 	
 Q() = 	
b) P() + Q() = 	 P() – Q() = 	
(0,25 điểm)
(0,25 điểm)
(0,75 điểm)
(0,75 điểm)
C©u 5.
Đa thức M() = a + 5 – 3 có một nghiệm là nên . 	 
Do đó: a = 0 	 a 	 Vậy a = 2 
(0,25 điểm)
(0,25 điểm)
(0,25 điểm)
(0,25 điểm)
C©u 6.
Vẽ hình đúng. (0,5 điểm)	
a) Chứng minh được
 = (cạnh huyền - góc nhọn). 	
b) 	
Suy ra: BE là đường trung trực của đoạn thẳng AH. 
c) và có:
 = = 900 
 AE = HE ( = ) 
 = (đối đỉnh)
 Do đó = (g.c.g) 
 Suy ra: EK = EC (hai cạnh tương ứng). 
d) Trong tam giác vuông AEK: AE là cạnh góc vuông, KE là cạnh huyền 
 AE < KE. 	
Mà KE = EC ( = ).
Vậy AE < EC. 	
(0,5 điểm)
(0,5 điểm)
(0,5 điểm)
(0,25 điểm)
(0,5 điểm)
(0,25 điểm)
(0,25 điểm)
(0,25 điểm)