Giáo án môn Hình học 6 - Tiết 34: Ôn tập chương I
I/Mục tiêu :
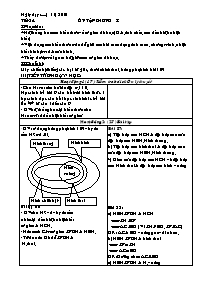
* Hệ thống hoá các kiến thức về tứ giác đã học (Đ/n, tính chất, các dấu hiệu nhận biết)
* Vận dụng các kiến thức trên để giải các bài toán dạng tính toán, chứng minh, nhận biết hình, tìm đ/k của hình.
* Thấy được mối quan hệ giữa các tứ giác đã học.
II/Chuẩn bị:
M¸y chiu hƯ thng c¸c lo¹i t gi¸c, thước hình thoi, bảng phụ hình bài 109
III/ Tin tr×nh d¹y - hc:
Bạn đang xem tài liệu "Giáo án môn Hình học 6 - Tiết 34: Ôn tập chương I", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Ngµy d¹y: ...../ 11 / 2010 TiÕt 24 «n tËp ch¬ng i I/Mục tiêu : * Hệ thống hoá các kiến thức về tứ giác đã học (Đ/n, tính chất, các dấu hiệu nhận biết) * Vận dụng các kiến thức trên để giải các bài toán dạng tính toán, chứng minh, nhận biết hình, tìm đ/k của hình. * Thấy được mối quan hệ giữa các tứ giác đã học. II/Chuẩn bị: M¸y chiÕu hƯ thèng c¸c lo¹i tø gi¸c, thước hình thoi, bảng phụ hình bài 109 III/ TiÕn tr×nh d¹y - häc: Hoạt động 1(17’): Kiểm tra bài cị ¤n lý thuyÕt - Cho Hs rút câu hỏi ôn tập tr.110. Häc sinh tr¶ lêi 9 c©u hái víi h×nh thøc 1 häc sinh ®äc c©u hái häc sinh kh¸c tr¶ lêi lÇn lỵt tø c©u 1 ®Õn c©u 9 - GV hệ thống hoá lại kiến thức cho Hsxem “sơ đồ nhận biết tứ giác” Hoạt động 2: (25’)Bµi tËp - GV sử dụng bảng phụ hình 109 và yêu cầu HS trả lời. H×nh vu«ng H×nh thang H×nh b×nh hµnh H×nh thoi H×nh ch÷ nhËt Bµi tËp 88 - GV cho HS vẽ và yêu cầu nhắc lại dấu hiệu nhận biết tứ giác là HCN. -Nêu cách C/m tứ giác EFGH là HBH. -Từ đó nêu Đk để EFGH là H.thoi. Bài 89: - Cho häc sinh VÏ hình và các nhóm thảo luận, Trình cách C/m ở từng câu. - GV nhận xét cách C/m của HS và tổng A B C M D E kết lại cách C/m. Híng dÉn häc sinh lµm bµi tËp 90 Bài 87: a) Tập hợp các HCN là tập hợp con của tập hợp các HBH, Hình thang. b) Tập hợp các hình thoi là tập hợp con của tập hợp các HBH, Hình thang. c) Giao của tập hợp các HCN và tập hợp các Hình thoi là tập hợp các hình vuông Bài 88: a) HBH EFGH là HCN EHEF ACBD (Vì EH // BD, EF//AC) ĐK: AC & BD vuông góc với nhau. b) HBH EFGH là hình thoi EF = EH AC = BD ĐK:Đường chéo ACBD c) HBH EFGH là H.vuông EFGH là HCN EFGH là H.thoi AC BD; AC = BD Bài tập 89: a) MD là đường trung bình của ABC và ACAB => MDAB Vậy AB là đường trung trực của ME nên E đối xứng M qua AB. b) EM //AC (1) EM = AC (2) (1) &(2) => AEMC là HBH c) AEBM là HBH =>AEBM là H.thoi. vàEM AB Chu vi H.thoi AEBM: BM x 4 = 8 (cm) d) AEBM là H.vuông => AB = EM AB =AC Ho¹t ®éng 3 (3’) Híng dÉn vỊ nhµ Xem l¹i c¸c bµi tËp ®· ch÷a HiĨu vµ thuéc ®Þnh nghÜa, tÝnh chÊt, dÊu hiƯu nhËn biÕt tø gi¸c lµ h×nh: thang, h×nh b×nh hµnh, h×nh ch÷ nhËt, h×nh thoi, h×nh vu«ng chuÈn bÞ tèt ®iỊu kiƯn ®Ĩ kiĨm tra 1 tiÕt vµo buỉi sau Lµm bµi tËp sau: Cho h×nh b×nh hµnh ABCD cã AB = 2AD , = 700. Gäi H lµ h×nh chiÕu cđa B trªn AD, M lµ trung ®iĨm cđa CD. TÝnh A B N D M C H E 700 Gi¸o viªn gỵi ý: VÏ h×nh, GT, KL Gäi N lµ trung ®iĨm AB, MN c¾t BH t¹i E. MN // AD vµ NA = NB NE HB t¹i E vµ EH = EB ME võa lµ ®êng cao võa lµ trung tuyÕn cđa MHB MH = MB vµ (1) MỈt kh¸c lµ h×nh thoi nªn = (2) Tõ (1) vµ (2) suy ra = 3.350 = 1050
Tài liệu đính kèm:
 T24 H8 ON CHUONG I t2.doc
T24 H8 ON CHUONG I t2.doc





