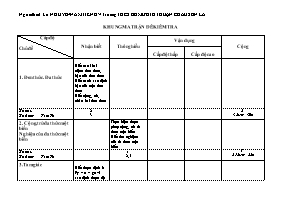
Khung ma trận đề kiểm tra

KHUNG MA TRẬN ĐỀ KIỂM TRA
 Cấp độ
Chủ đề 
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
1. Đơn thức. Đa thức
Biết các khái niệm đơn thức, bậc của đơn thức
Biết cách xác định bậc của một đơn thức
Biết cộng, trừ, nhân hai đơn thức
Số câu 
Số điểm Tỉ lệ %
2
3
2
3 điểm=30%
2. Cộng, trừ đa thức một biến
Nghiệm của đa thức một biến 
Thực hiện được phép cộng, trừ đa thức một biến
Biết tìm nghiệm của đa thức một biến
Số câu 
Số điểm Tỉ lệ %
1
2,5
1
2,5 điểm=25%
3.Tam giác
Biết được định lí Py – ta – go và xác định được độ dài một cạnh
Số câu 
Số điểm Tỉ lệ %
1
1
1
1,0 điểm = 10 %
4. Quan hệ giữa các yếu tố trong tam giác.
Các đường đồng quy của tam giác
Biết bất đẳng thức tam giác và viết được bất đẳng thức của một tam giác cụ thể
Chứng minh được hai tam giác bằng nhau. Vận dụng được mối quan hệ giữa cạnh và góc trong tam giác.
Vận dụng được tính chất các đường đồng quy của tam giác để chứng minh
Số câu 
Số điểm Tỉ lệ %
1
1
1
2,5
2
3,5 điểm=35%
Tổng số câu 
Tổng số điểm
Tỉ lệ %
4
5
50%
1
2,5
25%
1
2,5
25%
6
10
100%
PHÒNG GD&ĐT THUẬN CHÂU
Trường THCS Bó Mười B
CỘNG HOÀ XÃ HỘI CHỦ NGHĨA VIỆT NAM
Độc lập - Tự do - Hạnh phúc
=====o0o=====
ĐỀ KIỂM TRA HỌC KÌ II MÔN TOÁN NĂM HỌC 2010 – 2011
Thời gian: 90 phút
(Không kể thời gian chép đề)
Câu 1(1,5điểm):
 - Nêu định nghĩa đơn thức? Bậc của đơn thức?
	 - Lấy ví dụ về đơn thức và tìm bậc của đơn thức đó
Câu 2 (1điểm). Phát biểu định lí Py – ta – go. Xác định độ dài x trên hình vẽ?
Câu 3 (1điểm). Phát biểu định lí bất đẳng thức tam giác? Viết các bất đẳng thức tam giác về quan hệ giữa các cạnh của tam giác MNP.
Câu 4 (1,5điểm). Thực hiện phép tính:
a. (- 7x2y3) + 5x2y3 - 3x2y3
b. 9xy2 - 2xy2 - (- 3xy2)
c. xy2z . (- 3xyz2)
Câu 5 (2,5điểm) Cho hai đa thức:
P(x) = 2x5 - 3x2 + 5x4 - 7x3 + x2 - x
Q(x) = 3x4 - 2x5 - 3x3 + 2x2 - 
a. Sắp xếp các hạng tử của mỗi đa thức trên theo luỹ thừa giảm dần của biến.
b. Tính P(x) + Q(x) và P(x) - Q(x) 
c. Chứng tỏ rằng x = 0 là nghiệm của đa thức P(x) nhưng không phải là nghiệm của đa thức Q(x).
Câu 6 (2,5điểm). Cho ABC vuông tại A. Đường phân giác BK. Kẻ KH vuông góc với BC (HBC). Chứng minh răng:
	a) ABK = HBK.
	b) BK là đường trung trực của đoạn thẳng AH	
	c) AK < KC
PHÒNG GD&ĐT THUẬN CHÂU
Trường THCS Bó Mười B
CỘNG HOÀ XÃ HỘI CHỦ NGHĨA VIỆT NAM
Độc lập - Tự do - Hạnh phúc
=====o0o=====
ĐÁP ÁN VÀ BIỂU ĐIỂM HỌC KÌ II MÔN TOÁN 
NĂM HỌC 2010 – 2011
Thời gian: 90 phút
Câu
Lời giải
Điểm
Câu 1
Đơn thức là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và các biến.
0,5điểm
Bậc của đơn thức có hệ số khác 0 là tổng số mũ của tất cả các biến có trong đơn thức đó
0,5điểm
Ví dụ: - 5x2y3z, có bậc là 6 (Học sinh lấy ví dụ khác cũng được điểm)
0,5điểm
Câu 2
Định lí Py – ta – go: Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
0,5điểm
Theo định lí Py – ta – go ta có:
x2 + 82 = 102
Þ x2 = 102 - 82 = 100 – 64 = 36
Þ x = = 6
0,5điểm
Câu 3
Bất đẳng thức tam giác: Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại
0,5điểm
Các bất đẳng thức tam giác:
MN + MP > NP
MN + NP > MP
MP + NP > MN
0,5điểm
Câu 4
a. (- 7x2y3) + 5x2y3 - 3x2y3 = (- 7 + 5 – 3)x2y3 = -5x2y3
0,5điểm
b. 9xy2 - 2xy2 - (- 3xy2) = (9 - 2 + 3)xy2 = 10xy2
0,5điểm
c. xy2z . (- 3xyz2) = - 2x2y3z3
0,5điểm
Câu 5
a. Sắp xếp các hạng tử của mỗi đa thức theo luỹ thừa giảm dần của biến 
P(x) = 2x5 + 5x4 – 7x3 – 2x2 - x
Q(x) = - 2x5 + 3x4 - 3x3 + 2x2 - 
0,25điểm
0,25điểm
b. Tính P(x) + Q(x) và P(x) - Q(x) 
 +
 P(x) = 2x5 + 5x4 – 7x3 – 2x2 - x
 Q(x) = - 2x5 + 3x4 - 3x3 + 2x2 - 
 P(x) + Q(x) = 8x4 – 10x3 - x - 
0,5điểm
 -
 P(x) = 2x5 + 5x4 – 7x3 – 2x2 - x
 Q(x) = - 2x5 + 3x4 - 3x3 + 2x2 - 
 P(x) - Q(x) = 4x5 + 2x4 – 4x3 - 4x2 - x + 
0,5điểm
c. Khi x = 0 ta có: 
P(0) = 2.05 + 5.04 – 7.03 – 2.02 - .0 = 0
Vậy x = 0 là một nghiệm của đa thức P(x)
Q(x) = - 2.05 + 3.04 - 3.03 + 2.02 - = - 
Vậy x = 0 không là nghiệm của đa thức Q(x)
0,5điểm
0,5điểm
Câu 6
0,25điểm
GT ABC ( = 90o), BK là đường phân giác
 KH ^ BC; (HBC)
KL a) ABK = HBK.
	b) BK là đường trung trực của đoạn thẳng AH	
	c) AK < KC	
0,25điểm
Chứng minh:
a. Xét ABK và HBK vuông có: 
	ABK =HBK (GT)	 (1) 
	và BK cạnh chung 	 (2)
	Từ (1) và (2) ABK = HBK (cạnh huyền – góc nhọn) 
0,5điểm
b. Xét ABD và HBD có: 
	 BD chung 	 (3)
	ABD =HBD (GT) (4) 
 	Mặt khác, vì ABK = HBK nên BA = BH (5)
	Từ (3); (4) và (5) ABD = HBD (c.g.c)
	Khi đó: ADB =HDB và DA = DH
Lại có: ADB + HDB = 1800 nên ADB =HDB = 900
	Vậy BK là đường trung trực của AH (đpcm)
0,5điểm
0,5điểm
c. ABK = HBK nên AK = HK,
	Mặt khác trong KHC có HK < KC
	Vậy AK < KC (đpcm)
0,5điểm