Bài giảng môn học Lịch sử lớp 7 - Bài kiểm tra 1 tiết chương I

	BÀI KIỂM TRA 1 TIẾT CHƯƠNG I
	-------------	 (Hình học - Chương trình chuẩn)
I. Mục đích, yêu cầu:	 + Ôn tập, hệ thống và đánh giá việc lĩnh hội kiến thức hình chương I.
 + Hiểu rõ khái niệm về hình đa diện, vận dụng công thức để tính thể tích của khối đa diện
II. Mục tiêu:
+ Về kiến thức:	- Nắm được khía niệm về hình đa diện và khối đa diện, khối đa diện đều và thể tích của khối đa diện.
	- Nắm được phép dời hình trong không gian.
+ Về kỹ năng:	- Phân loại được khối đa diện đều.
	- Xác định được mặt phẳng đối xứng của khối tứ diện đều.
	- Tính được thể tích của khối đa diện và chiều cao của khối chóp.
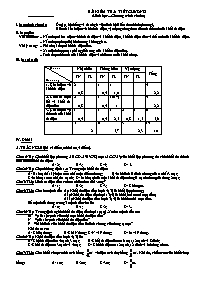
III. Ma trận đề:
 Mức độ
Nội dung
Nhận biết 
Thông hiểu
Vận dụng
Tổng
TN
TL
TN
TL
TN
TL
1. Khái niệm về khối đa diện
2
 0,8
1
 0,4
1
 1,0
4
 2,2
2. Khối đa diện lối và khối đa diện đều
2
 0,8
1
 0,4
1(Hv)
 1
4
 2,2
3. Khái niệm về thể tích của khối đa diện
1
 0,4
1
 0,4
1
 2,5
2
 0,8
1
 1,5
6
 5,6
5
 2
6
 5,7
3
 2,3
14
 10
IV. Đề bài:
A. TRẮC NGHIỆM: (4 điểm, mỗi câu 0,4 điểm).
Câu 1(NB): Cho khối lập phương ABCD.A’B’C’D’, mặt (ACC’A’) của khối lập phương đó chia khối đó thành bao nhiêu khối đa diện:	
	A/ 2;	B/ 3;	C/ 4;	D/ 5.
Câu 2(NB): Chọn khẳng định sai. Trong một khối đa diện:
	A/ Hai mặt bất kỳ luôn có ít nhất một điểm chung;	B/ Mỗi đỉnh là đỉnh chung của ít nhất 3 mặt;
	C/ Mỗi mặt có ít nhất ba cạnh;	D/ Mỗi cạnh của một khối đa diện cũng là cạnh chung của đúng 2 mặt;
Câu 3(TH): Hình tứ diện đều có bao nhiêu tâm đối xứng?
	A/ 1;	B/ 2;	C/ 3;	D/ Không có.
Câu 4(TH): Cho ba mệnh đề:	(I): Khối đa diện đều loại {4; 3} là khối lập phương;	
	(II): Khối đa diện đều loại {3; 5} là khối hai mươi mặt đều;	
(III): Khối đa diện đều loại {3; 4} là khối mười mặt đều.
	Số mệnh đề đúng trong 3 mệnh đề trên là:	
	A/ 0;	B/ 1;	C/ 2;	D/ 3.
Câu 5(NB): Trong định nghĩa khối đa diện đều loại {p; q}. Xét ba mệnh đề sau:
	M = “p là số cạnh của mỗi mặt khối đa diện đều”	
N = “p là số cạnh của khối đa diện đều”
	P = “Mỗi đỉnh của khối đa diện đều là đỉnh chung của đúng q mặt”
	Khi đó ta có:
	A/ Chỉ M đúng;	B/ Chỉ N đúng;	C/ N và P đúng;	D/ M và P đúng.
Câu 6(NB): Khối đa diện đều loại {4; 3} là:
	A/ Khối đa diện đều 4 cạnh, 3 mặt;	B/ Khối đa diện đều có 6 mặt, 12 cạnh và 8 đỉnh;
	C/ Khối đa diện có 3 cạnh và 4 mặt;	D/ Khối đa diện có 12 cạnh, 12 đỉnh và 6 đường chéo.
Câu 7(TH): Cho khối chóp có thể tích bằng m3 và diện tích đáy bằng m2. Khi đó, chiều cao của khối chóp bằng:	A/ 1m;	B/ 2m;	C/ 3m;	D/ m.
Câu 8(NB): Cho khối lăng trụ có diện tích đáy bằng và chiều cao bằng . Khi đó, thể tích của khối lăng trụ bằng:	
	A/ ;	B/ ;	C/ .	D/ S.h.
Câu 9(VD): Khi độ dài cạnh của một khối lập phương tăng lên k lần thì thể tích khối lập phương đó tăng lên:
	A/ k lần;	B/ 3k lần;	C/ k3 lần;	D/ k2 lần.
Câu 10(VD) Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh . SA vuông góc với đáy và SA = . Gọi I là trung điểm của SC. Thể tích khối chóp I.ABCD bằng:
	A/ ;	B/ ;	C/ ;	D/ .
B. TỰ LUẬN: (6 điểm)
	Cho tứ diện đều ABCD cạnh bằng 2a. Gọi M là trung điểm của CD.
	1/ Chỉ ra một mặt phẳng đối xứng của tứ diện ABCD (Không yêu cầu chứng minh) 
	2/ Tính thể tích của khối tứ diện ABCD.
	3/ Tính khoảng cách từ điểm M đến mp(ABC).
- - - - - - - - - - - - @ - - - - - - - - - - - -
V. Đáp án và biểu điểm:
Câu
1
2
3
4
5
6
7
8
9
10
Đáp án
A
A
D
C
D
B
B
D
C
A
A. TRẮC NGHIỆM: 	
B. TỰ LUẬN:
Hình vẽ (1 điểm) 
Tứ diện: 0,5 đ.
Phục vụ câu b: 0,5 đ.
1/ 1 điểm.
+ Chỉ ra được mặt phẳng (ABM) (hoặc một mặt khác) 	1,0 điểm.
2/ 2,5 điểm.
+ Ghi đúng công thức thể tích	0,5 điểm
+ Xác định và tính được chiều cao của khối tứ diện	1,0 điểm
+ Tính đúng diện tích đáy	0,5 điểm
+ Tính đúng thể tích	0,5 điểm.
3/ 1,5 điểm
+ Tính đúng thể tích khối tứ diện ABCM	0,5 điểm
+ Áp dụng công thức thể tích của tứ diện ABCM để 
suy ra khoảng cách từ M đến mp(ABC)	0,25 điểm.
+ Tính đúng kết quả khoảng cách	0,25 điểm
	Chú ý:	Nếu học sinh giải cách khác thì giáo viên căn cứ vào bài làm của học sinh mà cho điểm cho từng câu đúng với biểu điểm ở trên.