Đề thi học học kì I môn: Toán – lớp 7

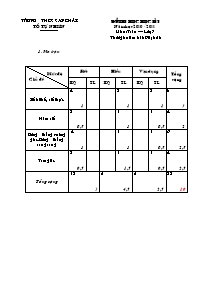
Trường thcs sán chải
tổ tự nhiên
đề thi học học kì i 
Năm học 2010 - 2011
Môn: Toán – Lớp 7
Thời gian làm bài: 90 phút.
1. Ma trận
 Mức độ
 Chủ đề
Biết
Hiểu
Vận dụng
Tổng cộng
KQ
TL
KQ
TL
KQ
TL
Số hữu tỉ, số thực
4
 1
2
 1
2
 1
8
 3
Hàm số
2
 0,5
1
 1
1
 0,5
4
 2
Đường thẳng vuông góc. Đường thẳng song song
 4
 1 
1
 1 
1
 0,5
6
 2,5
Tam giác
2
 0,5
1
 1,5
1
 0,5
4
 2,5
Tổng cộng
12
 3
5
 4,5
5
 2,5
22
 10
Trường thcs sán chải
tổ tự nhiên
đề thi học học kì i 
Năm học 2010 - 2011
Môn: Toán – Lớp 7
Thời gian làm bài: 90 phút.
Câu 1 (2đ). Mỗi câu sau đúng hay sai ?
	A. Q ⊂ R ; 	
B. Khi viết toạ độ của một điểm, ta viết tung độ trước.
C. Đường thẳng vuông góc với một đoạn thẳng là đường trung trực của đoạn thẳng ấy.
D. Mọi số hữu tỉ đều viết được dưới dạng số thập phân. 
E. Q ⊂ I
F. Mọi điểm trên trục tung đều có hoành độ bằng 0.
Câu 2 (1đ) Điền từ, cụm từ thích hợp vào chỗ trống trong các câu sau:
Hai đường thẳng phân biệt nếu không cắt nhau thì .
Hai tam giác có các cạnh tương ứng bằng nhau thì .
Số vô tỉ là những số viết được dưới dạng số thập phân vô hạn .
Nếu a và b cùng vuông góc với c thì 
Có . trường hợp bằng nhau của hai tam giác thường.
Phần khẳng định của một định định lí là . của định lí đó.
Câu 3(2đ). Thực hiện các phép tính:
	a) 12 + -34 ; 	b) 38 - -16 ; 
	c) 511 + 613 ∙ 1311; 	d) 723 ∙ 1419 + 723 ∙ 519 ;
Câu 3 (1,5đ). Cho hàm số y = f(x) = 2x + 1 ;
Tính: f(- 1) ; f(0) ; f(1) ; f(2).
Tìm giá trị của biến x để y = 7.
Câu 4: (1,5đ) Cho hình vẽ bên. Biết a // b.
A4 = 370. 
Tính số đo các góc: A1 , B2 , A3 , B1
Để góc B4 có số đo 1200 thì góc A1 phải có số đo bằng bao nhiêu độ ?
Câu 5 (2đ). 	
Cho hình vẽ bên, biết AB = AC; BAD = CAD .
a) Chững minh rằng: ∆ABD = ∆ACD ;
b) Biết góc ABD có số đo bằng 950, tính số đo góc ACD.
(Cán bộ coi thi không giải thích gì thêm)
Trường thcs sán chải
tổ tự nhiên
Hướng dẫn chấm thi học kì I
Năm học 2009 – 2010
Môn: Toán – Lớp 7
Cách chấm:
- Học sinh làm đúng phần nào chấm điểm phần đó.
- Học sinh làm cách khác đúng vẫn chấm điểm tối đa.
- Chấm theo thang điểm 10.
2. Đáp án
Câu
Nội dung
Điểm
1
Chọn chính xác mỗi ý, chấm 0,25 điểm
A. Đúng ; B. Sai ; C. Sai ; D. Đúng ; E. Sai ; F. Đúng
1,5đ
2
Điền đúng mỗi ý, chấm 0,25 điểm.
a) song song ; b) bằng nhau ; c) không tuần hoàn
d) a // b ; e) 3 ; f) kết luận
1,5đ
3
12 + -34 = -14 
38 - -16 = -14 
511 + 613 ∙ 1311 = 511 + 611 = 1
723 ∙ 1419 + 723 ∙ 519 = 723 ∙ 1419+519 = 723 ∙ 1 = 723 
0,5đ
0,5đ 
0,5đ
0,5đ
4
a) Tính được số đo mỗi góc, chấm 0,25 đ
A1 = 1430, B2 = 1430, A3 = 1430, B1 = 370.
b) A4 = 600
1 đ
0,5đ
6
Viết đúng GT, KL, chấm 0,25 điểm
0,25đ
0,25đ
0,25đ
0,25đ
0,5đ
0,5đ
GT
∆ABD và ∆ACD , AB = AC
BAD = CAD , ABD = 950
KL
a) ∆ABD = ∆ACD
b) ACD = ?
Chứng minh
a) Xét ∆ABD và ∆ACD, ta có:
AB = AC (GT)
BAD = CAD (GT)
AD là cạnh chung
Do đó: ∆ABD = ∆ACD (c . g . c)
b) Ta có: ACD = ABD (Hai góc tương ứng).
Vậy: ACD = 950