Đề và đáp án thi học sinh giỏi môn Toán lớp 9 - Đề số 28
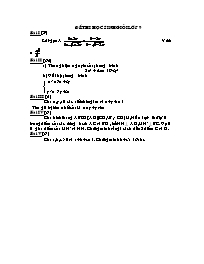
Bài III (3đ)
Cho x,y,z là các số không âm và x+y+z =1
Tìm giá trị lớn nhất của M = xy+yz+zx
Bài IV (6đ)
Cho hình thang ABCD (AD//CD,AB ≠₡ CD) M,N lần lượt thứ tự là trung điểm của các đường hcéo AC và BD , kẻ NH ⊥Û AD, MH ⊥Û BC. Gọi I là giao điểm của MH và NH. Chứng minh rằng I cách đều 2 điểm C và D.
Bài V (3đ)
Cho a,b,c >0 và a+b+c = 1. Chứng minh b+c ≥ 16abc.
Bạn đang xem tài liệu "Đề và đáp án thi học sinh giỏi môn Toán lớp 9 - Đề số 28", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Đề thi học sinh giỏi lớp 9 Bài I (2đ) Rút gọn A Với a = Bài II (6đ) a) Tìm nghiệm nguyên của phương trình 2x2 + 4x = 19-3y2 b) Giải hệ phương trình x3 =7x +3y y3 = 7y+3x Bài III (3đ) Cho x,y,z là các số không âm và x+y+z =1 Tìm giá trị lớn nhất của M = xy+yz+zx Bài IV (6đ) Cho hình thang ABCD (AD//CD,AB ≠ CD) M,N lần lượt thứ tự là trung điểm của các đường hcéo AC và BD , kẻ NH ⊥ AD, MH’ ⊥ BC. Gọi I là giao điểm của MH’ và NH. Chứng minh rằng I cách đều 2 điểm C và D. Bài V (3đ) Cho a,b,c >0 và a+b+c = 1. Chứng minh b+c ≥ 16abc.
Tài liệu đính kèm:
 5B.doc
5B.doc 5B_DA.doc
5B_DA.doc





