Giáo án Hình học 6 - Tiết 40: Tính chất đường phân giác của tam giác
I .Mục tiêu:
- Nắm vững nội dung định lý về tính chất đường phân giác của tam giác ,hiểu được cách cm trường hợp AD là tia phân giác của góc A.
- Vận dụng định lý giảI được các bài tập SGK (tính độ dài các đoạn thẳng và cm hình học)
II .Chuẩn bị:
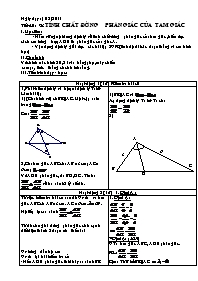
Vẽ chính xác hình 20, 21 vào bảng phụ, máy chiếu
compa, thước thẳng có chia khoảng.
III .Tiến trình dạy - học:
Bạn đang xem tài liệu "Giáo án Hình học 6 - Tiết 40: Tính chất đường phân giác của tam giác", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Ngày dạy: / 02/ 2011 Tiết 40 : Đ3 Tính chất đường phân giác của tam giác I .Mục tiêu: - Nắm vững nội dung định lý về tính chất đường phân giác của tam giác ,hiểu được cách cm trường hợp AD là tia phân giác của góc A. - Vận dụng định lý giảI được các bài tập SGK (tính độ dài các đoạn thẳng và cm hình học) II .Chuẩn bị: Vẽ chính xác hình 20, 21 vào bảng phụ, máy chiếu compa, thước thẳng có chia khoảng. III .Tiến trình dạy - học: Hoạt động 1 (15’) Kiểm tra bài cũ 1, Phát biểu định lý và hệ quả định lý Talét Làm bài tập 1) (Cho hình vẽ) có BE//AC. Một cặp sole trong Cm: 2,Cho tam giác ABC có: AB = 3cm; AC = 6cm ; Vẽ AD là phân giác, đo BD, DC . Tính: rồi so sánh 2 tỷ số đó. 1) BE//AC vì áp dụng định lý Ta let Ta có: A B C D 6 3 2) Hoạt động 2 (15’) 1. Định lý : Từ việc kiểm tra bàI củ sau đó Gv đưa ra tam giác ABC có AB =3cm. AC =6cm. =600. H/s tiếp tục so sánh Từ đó có nghĩa đường phân giác chia cạnh đối diện thành 2 đoạn như thế nào? Gv hướng dẩn h/s cm Gv đưa lại bàI kiểm tra củ - Nếu AD là phân giác thid hãy so sánh BE với AB? Từ đó em suy ra đIều gì? - Để chứng minh định lý này ta phải làm như thế nào? (Kẻ thêm đường BE//AC) 1. Định lý : *Định lý: (SGK) GT: tam giác ABC, AD là phân giác. KL: C/m: Từ B kẻ BE//AC Mà (gt) Vì AD là phân giác . tam giác ABE cân tại B AB = BE Theo hệ quả của định lý Talét ta có: (đpcm) Hoạt động 3 (5’) Chú ý - Định lý vẫn đúng trong trường hợp AD là phân giác góc ngoài của tam giác) *Chú ý: (SGK) AD là phân giác góc ngoàI của tam giác ABC thì: Hoạt động 4 (8’) Luyện tập củng cố 1, H/s nhắc lại tính chất đường phân giác của tam giác. 2, Làm bài tập: Cho tam giác ABC có: AB = 4,5 cm. AC = 7,2 cm. BD =3,5cm. Tính BC . AD là phân giác. 3, Cho tam giác ABC có AD là phân giác ngoài của tam giác ABC. Và AB = 6,2 ; AC = 8,7; DB = 2,5. Tính BC. 4, Bài tập 16(SGK) Hoạt động 5 (2’) Hướng dẫn học ở nhà Học thuộc định lý về tính chất đường phân giác trong tam giác. - Để xác định AD có phải là phân giác không ta làm thế nào? - Làm bài tập: 17,18,19 SGK. 17,18 SBT Tiết sau luyện tập.
Tài liệu đính kèm:
 H8 T40 TINH CHAT DUONG PHAN GIAC.doc
H8 T40 TINH CHAT DUONG PHAN GIAC.doc





