Giáo án môn Hình học 7 năm 2006 - Tiết 33: Luyện tập 1

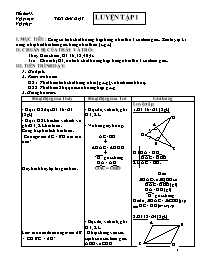
LUYỆN TẬP 1
Tiết thứ:33
Ngày soạn: 	 TÊN BÀI DẠY
Ngày dạy:
I. MỤC TIÊU: Củng cố tính chất trường hợp bằng nhau thứ 3 của tam giác. Rèn luyện kĩ năng nhận biết hai tam giác bằng nhau theo (c.g.c)
II. CHUẨN BỊ CỦA THẦY VÀ TRÒ:
	Thầy: Đèn chiếu, BT 36, 38,40,41.
	Trò: Chuẩn bị BT, ôn tính chất trường hợp bằng nhau thứ 3 của tam giác.
III. TIẾN TRÌNH DẠY:
Ổn định:
Kiểm tra bài cũ: 
	HS 1: Phát biểu tính chất bằng nhau (g.c.g), vẽ hình minh hoạ.
	HS 2: Phát biểu 2 hệ quả của trường hợp g.c.g
3. Giảng bài mới:
Hoạt động của Thầy
Hoạt động của Trò
Ghi bảng
- Gọi 1 HS đọc BT 36/123 (Sgk)
- Gọi 1 HS khác lên vẽ hình và ghi GT, KL bài toán.
Cùng hs phân tích bài toán.
 Chứng minh AC = BD như thế nào?
Hãy trình bày lại lời giải trên.
Làm thế nào để chứng minh AB = CD, BC = AD?
Có thể chúng minh các tam giác đó theo truờng hợp bằng nhau nào của hai tam giác, ta cần phải chỉ ra các tam giác đó thoả mãn những điều kiện nào?
- Hãy trình bày lại bài toán trên.
Bài 40/124(Sgk)
 Làm thế nào để so sánh BE, CF ?
- Đọc đề, vẽ hình, ghi GT, KL
- Vẽ trên giấy trong.
	 AC=BD
	 ñ	
 DOAC = DODB
	 ñ
 O : góc chung
 OA = AB
 OAC = OBD
- Đọc đề, vẽ hình, ghi GT, KL
 Ghép chúng vào các cạnh của các tam giác ABD và CDB
 AB = CD, AC = BD
 ñ
 ABC = DCB.
 ñ
 ABC = DCB 
 BC cạnh chung
 ABC = DCB 
 BE=CF
 ñ
 BEM = CFM
 E = F(=900)
 MB = MC
 BME = CMF
Luyện tập:
1. BT 36/123 (Sgk)
C
B
D
A
O
GT OA = OB
 OAC = OBD
KL AC = BD.
Giải:
 OAC và OBD có:
	OAC = OBD (gt)
	OA = OB (gt)
	 O : góc chung
Do đó, OAC = CBD (g.c.g)
 OC = OD (cạnh tương ứng).
A
C
D
B
2.BT 38/124 (Sgk)
GT AB // CD
 AC // BD
KL AB = CD
 AC = BD
Giải.
Nối C với B.
Xét ABC và DCB
ABC = DCB (cặp góc sole trong của AC // BD)
BC cạnh chung.
ABC = DCB (cặp góc sole trong của AC // BD)
Vậy ABC = DCB 
Do đó AB = CD (cặp cạnh tương ứng)
AC = BD (cặp cạnh tương ứng)
3.Bài 40/124(Sgk)
GT MB= MC, BE Ax
 CF Ax
KL so sánh BE = CF
 Giải:
 BEM và CFM có:
 E = F(=900)
 MB = MC (giả thiết)
 BME = CMF (đối đỉnh)
Do đó, BEM và CFM (cạnh huyền- góc nhọn)
Suy ra BE = CF (Hai cạnh tương ứng)
	4. Củng cố: qua luyện tập
B
5.BT về nhà: Làm BT 39, 40, 41, 42/124 (Sgk), chuẩn bị kiểm tra 15’
D
E
C
A
F
I
6.Hướng dẫn học ở nhà:bài 41/124(Sgk)
IBD=IBEID=IE
ICE=ICFIF=IE
ID=IE=IF