Giáo án môn Hình học 7 năm 2006 - Tiết: Luyện tập
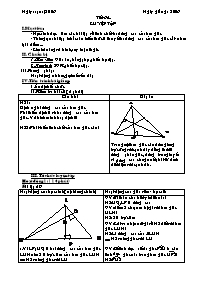
I.Mục tiêu:
-Học sinh được làm các bài tập về tính chất ba đường cao của tam giác
-Thông qua bài tạp khắc sâu kiến thức lí thuyết ba đường cao của tam giác cắt nhau tại1 điẻm.
-Rèn kĩ năng vẽ hình, suy luận lôgic
II. Chuẩn bị:
1.Giáo viên: Giáo án, bảng phụ,phiếu học tập.
2.Học sinh: SGK,phiếu học tập.
III. Phương pháp:
Hoạt động nhóm, gợi mở vấn đáp
Bạn đang xem tài liệu "Giáo án môn Hình học 7 năm 2006 - Tiết: Luyện tập", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Ngày soạn: /2006 Ngày giảng: 2006 Tiết 64. luyện tập I.Mục tiêu: -Học sinh được làm các bài tập về tính chất ba đường cao của tam giác -Thông qua bài tạp khắc sâu kiến thức lí thuyết ba đường cao của tam giác cắt nhau tại1 điẻm... -Rèn kĩ năng vẽ hình, suy luận lôgic II. Chuẩn bị: 1.Giáo viên: Giáo án, bảng phụ,phiếu học tập. 2.Học sinh: SGK,phiếu học tập. III. Phương pháp: Hoạt động nhóm, gợi mở vấn đáp IV. Tiến trình bài giảng. I .ổn định tổ chức. II. Kiểm tra bài cũ ( 5 phút) Câu hỏi Đáp án HS1: Định nghĩa đường cao của tam giác Phát biểu định lí vê ba đường cao của tam giác. Vẽ hình minh hoạ định lí? HS2: Phát biểu tính chất của tam giác cân? Trongmột tam giác cân đườngtrung trực ứng vớicạnh đáy đồng thời là đường phân giác, đường trung tuyến và đường cao cùng xuất phát từ đỉnh đối diện với cạnh đó. III. Tổ chức luỵện tập Hoạt động 1: ( 14 phút) Bài tập 59 Hoạt động của học sinh( nội dung chính) Hoạt động của giáo viên- học sih a.Vì LP; MQ là hai dường cao của tam giác LMN nên S là trực tâm của tam giác LMN NS vuông góc với LM b. Ta có PMS = 900- N= 900- 500= 400 theo tính chất về tổng ba góc trong tam giác ta cóo PSM= 900- PMS = 900- 400= 500 GV:Bài toán cho biết yêú tố nào? HS:MQ, LP là đường cao GV: điểm S có quan hệ gì với tam giác MLN? HS: S là trực tâm GV: Rút ra nhận xét gì về NS đối với tam giác LMN? HS:Là đường cao của LMN NS vuông góc với LM GV:Để tính dược số đo góc PSM ta càn tính được góc nào trong tam giác MPS? HS:PMS GV:Nêu cách tính PMS HS:PMS= 1800-( 900+500)= 400. Hoạt động 2: ( 16 phút) Bài tạp 55/80 Hoạt động của học sinh Hoạt động của giáo viên Bài giải: D thuộc dường trung trực của AB nên: DA=DB suy ra B= A1. Do đó ADB = 1800-2A1 D thuộc dường trung trực của AC nên: DA=DC suy ra C= A2. Do đó ADC = 1800-2A2 Suy ra: ADB + ADC= 3600-2( A1+A2)= 1800 Hay ba điểm B,C,D thẳng hàng Học sinh hoạt động cá nhân trong 4 phút Giáo viên vấn đáp, gợi mở: 12 phút GV: Để chứng minh B,C,D thẳng hàng ta làm như thé nào: Học sinh suy nghĩ trả lời. GV hướng dãn -Kẻ đường phụ BC,AD -Chứng minh cho góc DBC= 1800 GV: nêu cách chứng minh cho góc DBC = 1800? Tam giác BDA và CDA là tam giác gì? HS: tam giác cân Hãy tính BDA và CDA dựa vào T/C tỏng số đo ba góc trong tam giác? ADB = 1800-2A1 ADC = 1800-2A2 GV chốt lại: Qua bài toán trên các em càn ghi nhớ: -Trong tam giác vuông trrực tâm là trung diẻm cạnh huyền -Cách chứng minh ba điểm thẳng hành là góc tạo bởi 3 điểm = 1800 Giáo viên chốt lại kiến thức M TT của AB AM= BM 4 :Củng cố- 3 phút Qua bài luyện tạp hôm nay cần ghi nhớ: -Tính chất ba đường trung trực của tam giác - Có ba trường hợp của đường tròn đi qua ba đỉnh của tam giác: +Tâm nằm trong tam giác +Tâm nămg trên một cạnh của tam giác +Tâm nằm ngoài tam giác. -Trong tam giác vuông trung tuýen ứng với cạnh huyền bằng nửa cạnh huyền. 5 Kiểm tra đánh giá ( 5 phút) Bài tập: Tính dộ dài của trung truyến xuát phát từ dỉng góc vuông của tam giác vuông xuống cạnh huyền 6: Hướng dẫn về nhà ( 2 phút) -Học thuộc các định lí, tính chất các dường đồng quy đã học -Làm bài tập: 57 -Đọc trước bài Tính chất ba đường cao của tam giác.
Tài liệu đính kèm:
 T64.doc
T64.doc





