Giáo án Tự chọn Toán 7 - Tiết 15: Luyện tập về trường hợp bằng nhau thứ nhất của tam giác cạnh - Cạnh - cạnh (c. c. c)
- Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tan giác đó bằng nhau.
- Một tam giác hoàn toàn xác định khi biết ba cạnh của nó.
HS ôn tập các kiến thức.
Hoạt động 2: Luyện tập
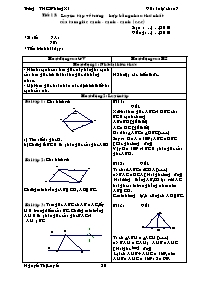
Bài tập 1: Cho hình vẽ:
a) Tìm số đo góc D.
b) Chứng tỏ BC là tia phân giác của góc ABD
Bài tập 2: Cho hình vẽ:
Chứng minh rằng: AB // CD, AD // BC.
Bài tập 3: Tam giác ABC có AB =AC, lấy M là trung điểm của BC. Chứng minh rằng AM là tia phân giác của góc BAC và
AM BC
Baứi taọp 4: Cho ABC . Veừ cung rroứn taõm A baựn kớnh BC, veừ cung troứn taõm C baựn kớnh BA, chuựng caỏt nhau taùi D ( D vaứ B naốm khaực phớa doỏi vụựi AC ). Chửựng minh raống AD // BC.
Baứi taọp 5: Cho goực xOÂy . Veừ cung troứn taõm O, cung naứy caột Ox , Oy theo thửự tửù taùi A vaứ B. Veừ cung troứn taõm A vaứ taõm B coự cuứng baựn kớnh sao cho chuựng caột nhau taùi ủieồm C. Noỏi O vụựi C. Chửựng minh raống OC laứ tia phaõn giaực cuỷa goực xOÂy
Bài 1:
Giải.
Xét hai tam giác ABC và DBC có:
BC là cạnh chung
AB =BD (giả thiết)
AC = DC (giả thiết)
Do đó: ABC = DBC (c.c.c)
Suy ra D =A = 1000; ABC = DBC
( Các góc tương ứng)
Vậy D = 1000 và BC là phân giác của góc ABD.
Bài 2: Giải.
Ta có: ABC = CDA (c.c.c)
=> BAC = DCA ( Hai góc tương ứng)
Hai đường thẳng AB,CD tạo với AC hai góc so le trong bằng nhau nên AB // CD.
C.minh tương tự, ta cũng có AD // BC.
Bài 3: Giải
Ta có ABM = ACM (c.c.c)
=> BAM = CAM ; AMB = AMC ( Hai góc tương ứng)
Lại có AMB + AMC = 1800, nên
AMB = AMC = 1800 : 2 = 900.
Vậy AM là tia phân giác của góc BAC và AM BC
Bài 4
Nối DA và DC
Xét 2 tam giác ABC vaứ ADC
Có AB = CD theo giả thiết
BC = AD theo giả thiết
Chung canh AC
Nên ABC = CDA
=>
=> AD // BC ( so le trong )
(ĐPCM)
Bài 5:
Xét 2 tam giác AOC vaứ BOC
Có AO = BO theo giả thiết
AC = BC theo giả thiết
Chung canh OC
Nên AOC = BOC
=>
=> OC laứ tia phaõn giaực cuỷa goực xOÂy
(ĐPCM)
Tiết 15: Luyện tập về trường hợp bằng nhau thứ nhất của tam giác cạnh - cạnh - cạnh (c.c.c) Soạn : ././2010 Giảng: ././2010 * Sĩ số: 7A: 7B: * Tiến trình bài dạy: Hoạt động của GV Hoạt động của HS Hoạt động 1: Nhắc lại kiến thức - Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tan giác đó bằng nhau. - Một tam giác hoàn toàn xác định khi biết ba cạnh của nó. HS ôn tập các kiến thức. Hoạt động 2: Luyện tập Bài tập 1: Cho hình vẽ: a) Tìm số đo góc D. b) Chứng tỏ BC là tia phân giác của góc ABD Bài tập 2: Cho hình vẽ: Chứng minh rằng: AB // CD, AD // BC. Bài tập 3: Tam giác ABC có AB =AC, lấy M là trung điểm của BC. Chứng minh rằng AM là tia phân giác của góc BAC và AM ^ BC Baứi taọp 4: Cho ABC . Veừ cung rroứn taõm A baựn kớnh BC, veừ cung troứn taõm C baựn kớnh BA, chuựng caỏt nhau taùi D ( D vaứ B naốm khaực phớa doỏi vụựi AC ). Chửựng minh raống AD // BC. Baứi taọp 5: Cho goực xOÂy . Veừ cung troứn taõm O, cung naứy caột Ox , Oy theo thửự tửù taùi A vaứ B. Veừ cung troứn taõm A vaứ taõm B coự cuứng baựn kớnh sao cho chuựng caột nhau taùi ủieồm C. Noỏi O vụựi C. Chửựng minh raống OC laứ tia phaõn giaực cuỷa goực xOÂy Bài 1: Giải. Xét hai tam giác ABC và DBC có: BC là cạnh chung AB =BD (giả thiết) AC = DC (giả thiết) Do đó: DABC = DDBC (c.c.c) Suy ra D =A = 1000; ABC = DBC ( Các góc tương ứng) Vậy D = 1000 và BC là phân giác của góc ABD. Bài 2: Giải. Ta có: DABC = DCDA (c.c.c) => BAC = DCA ( Hai góc tương ứng) Hai đường thẳng AB,CD tạo với AC hai góc so le trong bằng nhau nên AB // CD. C.minh tương tự, ta cũng có AD // BC. Bài 3: Giải Ta có DABM = DACM (c.c.c) => BAM = CAM ; AMB = AMC ( Hai góc tương ứng) Lại có AMB + AMC = 1800, nên AMB = AMC = 1800 : 2 = 900. Vậy AM là tia phân giác của góc BAC và AM ^ BC Bài 4 Nối DA và DC Xét 2 tam giác ABC vaứ ADC Có AB = CD theo giả thiết BC = AD theo giả thiết Chung canh AC Nên ABC = CDA => => AD // BC ( so le trong ) (ĐPCM) Bài 5: Xét 2 tam giác AOC vaứ BOC Có AO = BO theo giả thiết AC = BC theo giả thiết Chung canh OC Nên AOC = BOC => => OC laứ tia phaõn giaực cuỷa goực xOÂy (ĐPCM) Hoạt động 3: Hướng dẫn về nhà - Xem các bài tập đã chữa. - Để chứng minh hai đoạn thẳng , hai góc bằng nhau ta thường chứng minh chúng là các cạnh, các góc tương ứng của hai tam giác bằng nhau. Bài tập về nhà: Vẽ tam giác ABC biết: ba cạnh bằng 3 cm. Tiết 16: Luyện tập về trường hợp bằng thứ hai của tam giác cạnh - góc - cạnh (c.g.c) Soạn : ././2010 Giảng: ././2010 * Sĩ số: 7A: 7B: * Tiến trình bài dạy: Hoạt động của GV Hoạt động của HS Hoạt động 1: Nhắc lại kiến thức - Nếu hai cạnh và góc xen giữa của tam giác này tương ứng bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau. HS ôn tập các kiến thức. Hoạt động 2: Luyện tập Bài tập 1: Vẽ tam giác ABC biết AB = 3 cm, BC = 2cm, ABC = 600. Bài tập 2: Cho góc xOy; B Oy; A Ox; OA = OB; Om là tia phân giác góc xOy. Lấy C Om. Chứng minh: DAOC = DBOC. GV nhắc lại trường hợp bằng nhau c.g.c của tam giác. Bài tập 3: Cho DAOB có OA = OB. Tia phân giác góc O cắt AB ở D. Chứng minh rằng: a) DA = DB OD ^ AB Baứi taọp 4 Cho ABC trung tuyeỏn AM . treõn tia AM laỏy ủieồm D sao cho AD = 2AM .Chửựng minh raống: AB // CD. AC // BD. Bài 1: - Vẽ AB = 3cm; - Vẽ ABx = 600.Trên Bx lấy điểm C: BC=2cm. Nối A với C ta được tam giác ABC. Bài 2: Giải Xét DAOC và DBOC có: Ô1 = Ô2 ( gt) OA = OB ( gt) OC cạnh chung => DAOC = DBOC ( c.g.c) Bài 3 HS vẽ hình, ghi gt,kl: Chứng minh Xét tam giác AOD và BOD có: OA = OB (gt) Ô1 = Ô2 ( OD là phân giác góc O) OD là cạnh chung. => DAOD = DBOD (c.g.c) => AD = BD ( Cạnh tương ứng) b) Vì DAOD = DBOD. => D1 = D2 ( Hai góc tương ứng) Mà D1 + D2 = 1800 ( hai góc kề bù) => D1 = D 2 = 1800 : 2 = 900. Hay AD ^ AB. B C M A D Xeựt 2 tam giaực BMAvaứ CMD Coự BM = MC vaứ AM = DM do ủoỏi ủổnh Hai tam giaực baốờng nhau AB // CD Do so le trong Hoạt động 3: Hướng dẫn về nhà Xem các bài tập đã chữa. - BTVN: Baứi taọp 7: Cho ABC veừ ủoaùn thaỳng AD vuoõng goực vaứ baống AB ( D, C khaực phớa ủoỏi vụựi AB), veừ ủoaùn thaỳng AE vuoõng goực vaứ baống AC ( E,B khaực phớa ủoỏi vụựi AC ) Chửựng minh raống: CD = BE. CD BE. Baứi taọp 8: Cho ABC , goùi D, E theo thửự tửù laứ trung ủieồm cuỷa AC, AB. Treõn tia BD laỏy ủieồm M sao cho BM = 2 BD, treõn tia CE laỏy ủieồm N sao cho E laứ trung ủieồm cuỷa CN. Chửựng minh raống MN = 2 BC - Chuẩn bị các bài tập về hai tam giác bằng nhau trường hợp g.c.g Tiết 17: Luyện tập về trường hợp bằng nhau thứ ba của tam giác góc -cạnh - góc (g.c.g) Soạn : ././2010 Giảng: ././2010 * Sĩ số: 7A: 7B: * Tiến trình bài dạy: Hoạt động của GV Hoạt động của HS Hoạt động 1: Nhắc lại kiến thức - Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau. - Các hệ quả: + Hệ quả 1: Trường hợp cạnh góc vuông và góc nhọn kề cạnh ấy. + Hệ quả 2: Trường hợp cạnh huyền góc nhọn. HS ôn tập các kiến thức. Hoạt động 2: Luyện tập Bài tập 1: Trên mỗi hình vẽ a, b có các tam giác nào bằng nhau? Vì sao? - GV chốt trường hợp bằng nhau g.c.g. Bài tập 2: Cho tam giác ADE có D = Ê. Tia phân giác của góc D cắt AE tại M. Tia phân giác góc E cắt AD tại N. So sánh độ dài DN và EM. - GV yêu cầu HS vẽ hình, ghi gt, kl. ? So sánh hai đoạn thẳng ntn? Bài tập 3: Cho hình vẽ, trong đó: AB//HK; AH//BK. Chứng minh rằng: AB = HK; AH = BK. GV nêu nhận xét: Cặp đoạn thẳng song song bị chắn giữa hai đường thẳng song song thì bằng nhau. Bài 4: Cho hai điểm A và D nằm trên đường trung trực AI của đoạn thẳng BC. D nằm giữa hai điểm A và I, I là điểm nằm trên BC. Chứng minh: a. AD là tia phân giác của góc BAC b. ABD = ACD A B I C Bài 1: HS quan sát hình vẽ, trả lời: a) DABD = DACE (g.c.g) vì: D = Ê ( gt); DB = CE (gt); ABD = ACE ( cùng bù hai góc bằng nhau). + DABE = DACD (g.c.g) vì: B = C; BE = CD; Ê = D. b) DQMP = DNPM (g.c.g) vì: M =P =500; MP cạnh chung; P=M =700 Bài tập 2: HS vẽ hình, ghi GT, KL: Giải: Xét DDEN và DEDM có: NDE = MED (gt); DE cạnh chung; Ê1=D1 => DDEN = DEDM ( g.c.g) => DN = EM ( cặp cạnh tương ứng). Bài tập 3 HS quan sát hình vẽ, nêu hướng chứng minh. Giải: Kẻ AK, ta có: AB //HK => Â1 = K1( so le trong); AH // BK => Â2 = B2( góc SLT). Do đó: DABK = DKHA ( g.c.g). Suy ra: AB = HK; AH = BK. Bài 4 a. Xét hai tam giác ABI và ACI chúng có: AI cạnh chung AIC = AIB = 1v IB = IC (gt cho AI là đường trung trực của đoạn thẳng BC) Vậy (c.g.c) BAI = CAI Mặt khác I là trung điểm của cạnh BC nên tia AI nằm giữa hai tia AB và AC Suy ra: AD là tia phân giác của góc BAC b. Xét hai tam giác ABD và ACD chúng có: AD cạnh chung Cạnh AB = AC (vì AI là đường trung trực của đoạn thẳng BC) BAI = CAI (c/m trên) Vậy (c.g.c) ABD = ACD (cặp góc tương ứng) Hoạt động 3: Hướng dẫn về nhà Ôn tập các trường hợp bằng nhau của hai tam giác. Xem lại các bài tập đã chữa; Làm bài: 53,54,55 SBT/104. Tiết 18: Luyện tập về các trường hợp bằng nhau của tam giác. Soạn : ././2010 Giảng: ././2010 * Sĩ số: 7A: 7B: * Tiến trình bài dạy: Hoạt động của GV Hoạt động của HS Hoạt động 1: Ôn tập kiến thức - GV cho HS nhắc lại các trường hợp bằng nhau của hai tam giác. - GV hệ thống các trường hợp bằng nhau của tam giác; các trường hợp bằng nhau của tam giác vuông. HS nhắc lại các trường hợp bằng nhau của tam giác. Hoạt động 2: Luyện tập Bài tập : Cho góc xOy ( khác 1800). Trên tia Ox lấy hai điểm A,B sao cho OA< OB. Trên tia Oy lấy hai điểm C, D sao cho OC = OB, OD = OA. Hai đoạn thẳng AC và BD cắt nhau tại E. Chứng minh rằng: AC = BD; DEAB = DEAD; OE là tia phân giác của góc xOy HS vẽ hình, ghi gt, kl. Giải: D OAC = D ODB ( c.g.c) Suy ra: AC = BD. Từ D OAC = D ODB suy ra:A1=D1; và C= B. Do Â1+Â2=D1+D2 = 1800 nên: Â2=D2. Lại có: AB = OB – OA; CD = OC – OD nên AB = CD. D EAB và D EDC có :C= B; Â2=D2 AB = CD.( Chứng minh trên) Nên D EAB = D EDC (g.c.g) c) Từ D EAB = D EDC nên EA = ED do đó:DOEA = DOED (c.c.c) =>DOE= AOE Suy ra OE là phân giác của góc xOy. Cho ABC có AC > AB . Trên AC lấy điểm E sao cho CE = AB . Gọi O là 1 điểm sao cho OA = OC , OB = OE .C/m : a) AOB = COE b) So sánh các góc OAB và góc OCA Bài tập 2 ABC ; AC > AB EAC ; AB = CE GT OA = OC ; OB = OE a) AOB = COE KL b) So sánh các góc OAB và góc OCA HS phân tích tìm lời giải theo nhóm a) Xét AOB và COE có AB =CE ( gt) ; AO = CO ( gt) ; OB = OE (gt) AOB = COE (c-c-c) b) theo câu a thì AOB = COE nên ( góc tương ứng) Hoạt động 3: Kiểm tra viết 20 phút. Đề bài: Bài 1: Cho tam giác ABC có B = C. Tia phân giác góc A cắt BC tại D. Chứng minh : AB = AC. Bài 2: Cho hình vẽ, chứng minh rằng O là trung diểm của mỗi đoạn AD, BC. Hoạt động 4: Hướng dẫn về nhà: - Xem lại các bài tập đã chữa. - Ôn tập các kiến thức của trong học kì I chuẩn bị cho bài KT học kì. - Làm bài 58,59,60 SBT/105.
Tài liệu đính kèm:
 chu de 3 tiep.doc
chu de 3 tiep.doc





