Tóm tắt lý thuyết Toán 7 học kỳ 2
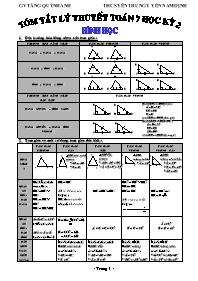
TRƯỜNG HỢP BẰNG NHAU TAM GIÁC THƯỜNG TAM GIÁC VUÔNG
CẠNH – CẠNH – CẠNH
CẠNH – GÓC – CẠNH
GÓC – CẠNH – GÓC
TRƯỜNG HỢP BẰNG NHAU
ĐẶC BIỆT TAM GIÁC VUÔNG
CẠNH HUYÊN – GÓC NHỌN
Bạn đang xem 20 trang mẫu của tài liệu "Tóm tắt lý thuyết Toán 7 học kỳ 2", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Các trường hợp bằng nhau của tam giác : TRƯỜNG HỢP BẰNG NHAU A B C D E F TAM GIÁC THƯỜNG TAM GIÁC VUÔNG CẠNH – CẠNH – CẠNH A B C D E F CẠNH – GÓC – CẠNH A B C D E F B A C E D F GÓC – CẠNH – GÓC B A C E D F TRƯỜNG HỢP BẰNG NHAU ĐẶC BIỆT Xét DABC và DDEF ta có :  = D = 900 BC = EF C = FÂ Þ DABC = DDEF ( ch – gn ) TAM GIÁC VUÔNG CẠNH HUYÊN – GÓC NHỌN B A C E D F Xét DABC và DDEF ta có :  = D = 900 BC = EF AC = DF Þ DABC = DDEF ( ch – cgv ) CẠNH HUYỀN – CẠNH GÓC VUÔNG B A C E D F Tam giác và một số dạng tam giác đặc biệt : TAM GIÁC THƯỜNG TAM GIÁC B C A CÂN TAM GIÁC C A B DABC đều suy ra: * AB = AC = BC *  = B = C = 600 ĐỀU TAM GIÁC VUÔNG TAM GIÁC DABC vuông cân tại A: *  = 900 * B = C = 450 * AB = AC VUÔNG CÂN ĐỊNH NGHĨA B C A A B C x DABC cân tại A suy ra: * AB = AC * B = C DABC vuông tại A: *  = 900 C A B QUAN HỆ GIỮA CÁC CẠNH Bất đẳng thức tam giác : BC < AB + AC AB < AC + BC AC < AB +BC AB = AC AH là đường cao Suy ra : AH là trung tuyến cũng là phân giác AB = BC = CA BC2 = AB2 + AC2 BC > AB BC > AC AM : trung tuyến Suy ra: AB = AC = a BC = QUAN HỆ GIỮA CÁC GÓC Â+BÂ+C = 1800 ( Tổng 3 góc ) ACÂx =  + B ( góc ngoài D ) B = CÂ=(1800–Â)  = 1800 – 2B = 1800 – 2C  = B = C = 600 B + C = 900  = 900 B = C = 450 DẤU HIỆU NHẬN BIẾT (chứng minh) Muốn chứng minh DABC cân tại A ta có 2 cách : * AB = AC * B = C Muốn chứng minh DABC đều ta có 2 cách : * AB = AC = BC *  = B = C Muốn CMR DABC vuông ta có 2 cách : *  = 900 * BC2 = AB2+AC2 Muốn CMR DABC vuông cân ta có 2 cách : * Â=900 và AB=AC * Â= 900 và BÂ= 450 Các tính chất liên quan đến quan hệ thứ tự giữa các độ dài đoạn thẳng hoặc số đo góc của tam giác : A B C HÌNH VẼ MÔ TẢ TÍNH CHẤT A D C H B d Trong DABC : BC là cạnh đối diện  AB là cạnh đối diện C AC là cạnh đối diện B 1. Quan hệ giữa góc và cạnh đối diện :  > B > CÂ Þ BC > AC > AB 2. Quan hệ giữa cạnh và góc đối diện : AB > BC > CA Þ C >  > B Cho đường thẳng d và A Ï d , AH ^ d B Ỵ d , C Ỵ d , D Ỵ d Ta nói : * H là hình chiếu của A trên d * AH là đường vuông góc kẻ từ A đến d * AB, AC, AD là đường xiên kẻ từ A đến d Quan hệ giữa đường vuông góc và đường xiên AH < AB , AH < AC , AH < AD Quan hệ giữa hình chiếu và đường xiên HD > HC Û AD > AC Quan hệ giữa hình chiếu và đuờng xiên HB = HC Û AB = AC Các tính chất cơ bản liiên quan đến đoạn thẳng và góc TRUNG ĐIỂM E A B d A M B M là trung điểm của AB Û AM = MB = AB ĐƯỜNG TRUNG TRỰC TC1 : Cho d là đường trung trực của đoạn thẳng AB Û d ^ AB và M là trung điểm của AB M TC2 : E nằm trên đường trung trực d Û EA = EB O x z y PHÂN GIÁC x z y O M A B TC1: TC2 : Û MA = MB Oz là tia phân giác của xÔy Oz là phân giác của xÔy Û xÔz = yÔz = xÔy MA ^ Ox và MB ^ Oy SONG SONG 1 B A 1 2 3 4 3 2 4 * So le trong : Â4 = BÂ2 ; Â3 = BÂ1 * Đồng vị : Â1 = BÂ1 ; Â2 = BÂ2 ; Â3 = BÂ3 ; Â4 = BÂ4 * Trong cùng phía : Â4 + BÂ1 = 1800 ; Â3 + BÂ2 = 1800 Các đường chủ yếu của tam giác và tính chất ĐƯỜNG CAO TRUNG TUYẾN TRUNG TRỰC PHÂN GIÁC A B H C Đường cao là đường thẳng từ đỉnh kẻ vuông góc với cạnh đối diện DABC có AH ^ BC. Ta nói : A H B C AH là đường cao A B C M Trung tuyến là đường thẳng kẻ từ đỉnh đến trung điểm của cạnh đối diện DABC có M là trung điểm của BC Ta nói : AM là trung tuyến Trung trực là đường thẳng vuông góc với đoạn thẳng tại trung điểm của đoạn thẳng đó A B M C d DABC có M là trung điểm của BC d qua M vuông góc BC Ta nói : d là đường trung trực của BC C B A D Phân giác là đường thẳng kẻ từ đỉnh và chia đều 2 góc của đỉnh đó DABC có AD chia  thành 2 góc Â1 = Â2 Ta nói : AD là phân giác của  TÍNH CHẤT CỦA ĐƯỜNG CHỦ YẾU TRONG TAM GIÁC DABC có : 3 đường cao AD, BE, CF đồng qui tại 1 điểm (cùng đi qua điểm H ) Điểm H được gọi là TRỰC TÂM của DABC A B C D E F H A B C D M N I d1 d2 d3 A B C A1 B1 C1 O A B C D M N G DABC có : 3 đường trung tuyến AD, BM, CN đồng qui tại 1 điểm ( cùng đi qua điểm G ) Điểm G được gọi là TRỌNG TÂM của DABC TÍNH CHẤT : * , * , * , DABC có : 3 đường trung trực d1 , d2 , d3 đồng qui tại 1 điểm ( cùng đi qua điểm I ) Điểm I được gọi là TÂM ĐƯỜNG TRÒN NGOẠI TIẾP của DABC TÍNH CHẤT : IA = IB = IC DABC có : 3 đường phân giác AA1, BB1, CC1 đồng qui tại 1 điểm ( cùng đi qua điểm O ) Điểm O được gọi là TÂM ĐƯỜNG TRÒN NỘI TIẾP của DABC TÍNH CHẤT : OH ^ AB ( H Ỵ AB ) OI ^ BC ( I Ỵ BC ) OK ^ AC ( K Ỵ AC ) Suy ra : OH = OI = OK ĐƠN THỨC ĐA THỨC ĐỊNH NGHĨA Đơn thức là biểu thức đại số chỉ gồm một số hoặc một biến, hoặc một tích giữa các số và các biến Ví dụ : ; ; ; ; ; Đa thức là tổng của những đơn thức. Mỗi đơn thức trong tổng được gọi là hạng tử của đa thức Ví dụ : ( đa thức A gồm 3 hạng tử ) BẬC , HỆ SỐ VÀ PHẦN BIẾN CỦA ĐƠN THỨC Bậc của đơn thức có hệ số khác 0 là tổng số mũ của tất cả các biến có trong đơn thức đó Ví dụ : 0 là đơn thức không có bậc – 5 là đơn thức có bậc 0 2x3y là đơn thức có bậc 4 – 3x2y3z là đơn thức có bậc 6 Bậc của đa thức thu gọn là bậc của hạng tử có bậc cao nhất Ví dụ 1: là đa thức có bậc 5 Ví dụ 2: là đa thức có bậc 6 Ví dụ 3: Thu gọn C ta có : Vậy đa thức C có bậc 4 ĐƠN THỨC ĐỒNG DẠNG Đơn thức đồng dạng là các đơn thức có hệ số khác 0 và có cùng phần biến Ví dụ : ; ; ; là những đơn thức đồng dạng Lưu ý: Các số khác 0 được coi là những đơn thức đồng dạng A CÁC DẠNG TOÁN CƠ BẢN 1. Thu gọn và chỉ ra bậc , hệ số và phần biến của đơn thức : Vậy : * Đơn thức A có bậc là 9 * Hệ số là * Phần biến là x3y3z3 B Vậy : * Bậc của đơn thức B là : 20 * Hệ số là : – 2 * Phần biến là : x7y5z8 2. Tính tích của hai đơn thức sau : và Giải Ta có : 3. Cộng , trừ các đơn thức : a) b) Tính giá trị của biểu thức : A = 2x3y – xy2 – 1 ( tại x = –1 , y = –2 ) Giải Thay x = –1 , y = –2 vào biểu thức A : A = 2(–1)3(–2) – (–1)( –2)2 – 1 = 2(–1).(–2) – (–1)(2) – 1 = 4 + 2 – 1 = 5 Cho hai đa thức : Thu gọn 2 đa thức P và Q Tính P + Q Tính Q – P Tìm đa thức C sao cho C + Q = P Giải Thu gọn đa thức : Tính P + Q Tính Q – P Tìm đa thức C sao cho C + Q = P Ta có : C + Q = P Û C = P – Q ( Thực hiện phép tính như câu c – HS tự làm ) ĐA THỨC MỘT BIẾN ĐỊNH NGHĨA Đa thức 1 biến là tổng của những đơn thức có cùng 1 biến Ví dụ : là đa thức của biến x là đa thức của biến y HỆ SỐ Xét đa thức đã được thu gọn : . 3 là hệ số của lũy thừa bậc 5 – 1 là hệ số của lũy thừa bậc 3 2 là hệ số của lũy thừa bậc 1 – 4 là hệ số của lũy thừa bậc 0 ( còn được gọi là hệ số tự do ) CỘNG TRỪ ĐA THỨC NGHIỆM CỦA ĐA THỨC Cho 2 đa thức : Thu gọn và sắp xếp các hạng tử của đa thức trên theo lũy thừa giảm dần của biến Tìm bậc , hệ số ca nhất ; hệ số tự do Tính A(x) + B(x) Tính C(x) – A(x) Giải Thu gọn và sắp xếp : Tìm bậc , hệ số của đa thức A(x) : Đa thức A(x) có : Bậc là 4 Hệ số cao nhất là 2 Hệ số tự do là 1 Tính A(x) + B(x) : Tính C(x) – A(x) Định nghĩa : Nếu tại x = a , đa thức P(x) có giá trị bằng 0 thì ta nói : x = a là nghiệm của đa thức Ví dụ : Cho đa thức Ta có : * Vậy x = – 2 là nghiệm của đa thức P(x) * Vậy x = – 3 không là nghiệm của đa thức Các Ví dụ về tìm nghiệm của đa thức : Ví dụ 1 : Cho đa thức f(x) = 2x + 5 Ta có : 2x + 5 = 0 Û 2x = 0 – 5 Û 2x = – 5 Û x = Vậy đa thức f(x) có nghiệm x = Ví dụ 2 : Cho đa thức g(x) = 2x2 – 50 Ta có : 2x2 – 50 = 0 Û 2x2 = 50 Û x2 = 25 Û x = 5 hoặc x = – 5 Vậy đa thức g(x) có nghiệm x = 5 hoặc x = – 5 Ví dụ 3 : Cho đa thức h(x) = x2 + 9 Ta có : x2 + 9 = 0 Û x2 = – 9 ( vô lý ) x Ỵ Ỉ Vậy đa thức h(x) không có nghiệm Ví dụ 4 : Cho đa thức k(x) = x2 + 9x Ta có : x2 + 9x = 0 Û x.(x + 9) = 0 Û x = 0 hoặc x + 9 = 0 Û x = 0 hoặc x = – 9 Vậy nghiệm của đa thức k(x) là x = 0 hoặc x = – 9 CHƯƠNG 2 : HÀM SỐ VÀ ĐỒ THỊ Đại lượng y có phải là hàm số của đại lượng x hay không ? Bảng các giá trị tương ứng của chúng là : x – 4 – 2 0 1 3 5 7 y – 9 – 5 – 1 1 5 9 13 Bảng các giá trị tương ứng của chúng là : x 0 2 4 6 8 10 12 y 6 6 6 6 6 6 6 Bảng các giá trị tương ứng của chúng là : x – 6 – 2 – 1 0 1 1 3 y 8 4 2 – 1 1 6 8 Hàm số y = f(x) được cho bởi công thức Hãy điền các giá trị tương ứng của hàm số y = f(x) vào bảng sau : X – 9 – 6 3 12 y= f(x) 1 Tính f(– 12) ; f(24) Cho hàm số y = f(x) = 2x – 1 Tính các giá trị ; ; ; Tìm x để f(x) = 3 Cho hàm số y = f(x) = 2x Tìm tọa độ các điểm A, B thuộc đồ thị của hàm số. Cho biết và Điểm nào sau đây thuộc đồ thị hàm số trên : A( 1 ; 2 ) ; B( – 2 ; 3 ) ; C( 1 ; 2 ) ; D( –2 ;–4 ) Cho hàm số : và Vẽ trên cùng một hệ trục tọa độ đồ thị của các hàm số Tìm hai điểm trên đồ thị của hàm số có tọa độ nguyên Cho hàm số : y = f(x) = ax + 3. Tìm a biết đồ thị hàm số đi qua điểm A( 2 ; – 1 ) y = f(x) = – 3x + b. Tìm b biết đồ thị của hàm số đi qua điểm M ( 1 ; – 2 ) Đại lượng y có phải là hàm số của đại lượng x hay không ? Nếu bảng giá trị tương ứng của chúng là : x -3 -2 -1 0 1 2 3 y -6 -4 -2 0 2 4 6 Nếu bảng giá trị tương ứng của chúng là : x -4 -2 0 1 3 5 7 y 8 8 8 8 8 8 8 Nếu bảng giá trị tương ứng của chúng là : x -8 -4 -4 -2 0 3 5 y 2 4 12 6 1 7 9 ... hân giác của  Cho góc xOy. Lấy các điểm A, B thuộc Ox sao cho OA > OB. Lấy các điểm C, D thuộc Oy sao cho OC = OA và OD = OB. Gọi E là giao điểm của AD, BC. CMR :AD = BC CMR :DABE = DCDE CMR : OE là tia phân giác của góc xÔy Cho DABC đường cao AH. Vẽ điểm D ao cho AB là đường trung trực của HD. Vẽ điểm E sao cho AC là đường trung trực của HE. DE cắt AB, AC tại I, K CMR : IB là tia phân giác của góc HID CMR : KC là tia phân giác của góc HKE CMR : HA là tia phân giác của góc IHK CMR : IC là tia phân giác của góc HIK và IC ^ AB CMR : KB là tia phân giác của góc HKI và KB ^ AC CHỨNG MINH Cho DABC cân tại A. CMR : trung tuyến AM đồng thời là phân giác (BT thuận) Cho DABC có trung tuyến AM đồng thời là phân giác. CMR : DABC cân (BT đảo) Cho DABC có phân giác AD, BE cặt nhau tại I. Vẽ IH ^ AB, IK ^ AC , IM ^ BC. CMR : DIHK cân CMR : DIKM cân CMR : DIMH cận TÍNH CHẤT BA ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC TÍNH TOÁN Cho DABC các đường phân giác BK, CH cắt nhau tại I. Tính  . Biết : BIÂC = 250 Cho DABC có  = 800 . Các đường phân giác BK, CH cắt nhau tại I Tính BÂI Tính BIÂC Cho DABC vuông tại A. AB= 3cm, BÂ= 600. Tính độ dài phân giác BD ( D nửa đều ) Cho DABC các đường phân giác BK, CH cắt nhau tại I. Tính  . Biết : BIÂC = 1210 Cho DABC có  = 600 . Các đường phân giác BK, CH cắt nhau tại I Tính BÂI Tính BIÂC Điểm I có cách đều ba cạnh của tam giác không ? tại sao ? Cho DABC vuông tại B. Tính độ dài phân giác BD AB = 6cm,  = 600 ( D nửa đều ) AB = 9cm, C = 300 ( D nửa đều ) AB = 3cm, BC = CHỨNG MINH Cho DABC các đường phân giác BK, CH cắt nhau tại I. CMR : BIÂC là góc tù Cho DABC cân tại A. Gọi G là trọng tâm của tam giác . Gọi I là giao điểm của các đường phân giác. CMR : ba điểm A, I, G thẳng hàng ( sử dụng bổ đề trong tam giác cân trung tuyến đồng thời là đường phân giác ) Cho DABC cân tại A. Các đường phân giác BD, CE cắt nhau tại I. CMR : AI đi qua trung điểm M của BC Cho DABC . Hai đường phân giác của góc BÂ, C cắt nhau tại I và hai đường phân giác của hai góc ngoài BÂ, C cắt nhau tại M. CMR : A, I, M thẳng hàng ( Sử dụng bổ đề của tia phân giác ) Cho DABC cân tại A. Gọi M là trung điểm của BC. Gọi E, F là chân các đường vuông góc kẻ từ M đến AB, AC. CMR : ME = MF Cho DABC có  = 1200 . Các đường phân giác AD, BE, CF CMR : DE là phân giác của góc ADÂC Tính EDÂF TÍNH CHẤT ĐƯỜNG TRUNG TRỰC CỦA ĐỌAN THẲNG BỔ ĐỀ M là điểm nằm trên đường trung trực của đọan thẳng AB. CMR : MA = MB Cho hai điểm M, N nằm ngoài đọan thẳng Ab sao cho MA = MB và NA = NB. CMR : MN là đường trung trực của AB CHỨNG MINH Cho DABC có hai đường trung trực của AB, AC cắt nhau tại I. CMR : I nằm trên đường trung trực của đọan BC Cho xÔy = 800 , điểm A nằm trong xÔy. Vẽ B sao cho Ox là đường trung trực của AB. Vẽ C sao cho Oy là đường trung trực của AC. CMR: O thuộc đường trung trực của BC Tính BÔC Cho ba tam giác cân chung đáy BC là DDBC, DEBC, DFBC. CMR : D, E, F thẳng hàng Cho hai điểm M, N nằm trên đường trung trực của AB. CMR : DAMN = DBMN Cho xÔy = 600 , điểm A nằm trong xÔy. Vẽ B sao cho Ox là đường trung trực của AB. Vẽ C sao cho Oy là đường trung trực của AC. CMR: OB = OC Tính BÔC Cho xÔy , điểm A nằm trong xÔy. Vẽ B sao cho Ox là đường trung trực của AB. Vẽ C sao cho Oy là đường trung trực của AC. Tính xÔy biết BÔC = 1100 Cho DABC có  = 600 . Các đường trung trực của AB và AC cắt nhau tại O. Tính số đo các góc ở đỉnh O TÍNH CHẤT BA ĐƯỜNG TRUNG TRỰC CỦA TAM GIÁC Cho DABC cân tại A. trung tuyến AM cắt đường trung trực của AC tại O. CMR: OA= OB Cho DABC có  tù. Các đường trung trực của AB, AC cắt nhau t5ai O và cắt BC tại D, E CMR : DABD và DACE cân. TÍNH CHẤT BA ĐƯỜNG CAO CỦA TAM GIÁC TÍNH TOÁN Cho DABC có AB = AC = 10cm, BC = 8cm. Tính đường cao AH Cho DABC có AB = AC = 13cm, BC = 10cm. Tính độ dài đuờng cao AH Cho DABC có AB = 3cm, AC = 4cm, BC = 5cm. Tính độ dài đuờng cao AH XÁC ĐỊNH TRỰC TÂM – VẼ TRỰC TÂM Cho DABC có trực tâm H. Tìm trực tâm của DABH, DACH, DBCH Cho DABC vuông tại A, đường cao AH CMR : A là trực tâm của DABC Tìm trực tâm của DABH và DACH Vẽ trực tâm của DABC trong các trường hợp sau : DABC nhọn DABC vuông tại A DABC tù CHỨNG MINH Cho DABC , gọi M, N, P là trung điểm của BC, AC, AB. CMR : các đường cao của DMNP là các đường trung trực của DABC Cho DABC cân tại A, Gọi M là trung điểm của BC. Kẻ đuờng cao BN cắt AM tại H CMR : CH ^ AB Tính số đo các góc BHÂM, MHÂN. Biết : C = 400 Cho DABC vuông tại A, đường cao AH. Gọi D, E là trung điểm của HC, HA. CMR : BE ^ AD Cho DABC có  = 450 và AC < BC, đuờng cao CE. Trên tia đối của tia CE lấy điểm D sao cho EB =ED. CMR : BC ^ AD Cho DABC có  = 450 và trực tâm H. CMR : BC = AH Cho DABC cân tại A, trung tuyến AM. Kẻ đường thẳng d qua A và vuông góc với AM. CMR : d // BC Cho DABC cân tại A, phân giác AM. Kẻ đường cao BN cắt AM tại H CMR : CH ^ AB Tính số đo các góc BHM , MHN . Biết C = 390 Cho DABC cân tại A, Gọi M là trung điểm BC. Kẻ đường cao BN cắt AM tại H CMR : CH ^ AB Tính số đo các góc BHM , MHN . Biết C = 500 Cho hai tam giác vuông DABC và DABD có chung cạnh huyền BC. Gọi H là giao điểm của AD , BC. Kẻ HK ^ AB. CMR : AC, BD, HK đồng quy Cho DABC cân tại A. Trên tia đối của tia AB lấy điểm D sao cho AB =AD. Kẻ đường cao AM của DABC và đường cao AN của DACD. CMR : DMAN vuông tại A Cho DABC. Qua mỗi đỉnh A, B, C vẽ các đường thẳng song song với cạnh đối diện. Chúng cắt nhau lần lượt tại M, N, P CMR : A là trung điểm của MP CMR : các đường cao của DABC là các đường trung trực của DMNP Cho DABC có  = 1350 và trực tâm H. CMR : BC = AH Cho DAbc có trực tâm H và AH = BC. Tính số đo góc  Cho DABC. Gọi D, E lần lượt là trung điểm của AB, AC. Trên tia DE lấy điểm F sao cho DE=DF. CMR: BD =CF DBCD = DFDC và DF =BC DE // và = ½ BC Cho góc xOy. Lấy các điểm A, B thuộc Ox sao cho OA > OB. Lấy các điểm C, D thuộc Oy sao cho OC =OA, OD =OB. Gọi E là giao điểm của AD, BC. CMR: AD = BC DABE =DCDE OE là phân giác của góc xÔy Cho DABC. D là trung điểm AB. Đường thẳng qua D song song với BC cắt AC tại E, đường thẳng qua E sogn song với AB cắt BC tại F. CMR: AD = EF DADE = DEFC suy ra AE =EC Cho DABC. Vẽ AD ^ AB và AD = AB ( D, C nằm khác phía đối với đường thẳng AB).Vẽ AE ^ AC và AE =AC (E, B nằm khác phía đối với đường thẳng AC). Nếu cho biết DE =BC. Tính góc BÂC CMR : A nằm giữa D, C BD // CE Cho đoạn thẳng MN có trung điểm H.Vẽ đường trung trực d của MN. Lấy P Ỵ d ( P ≠ H). CMR: PH là phân giác của góc MPN. Lấy Q sao cho P nằm giữa Q và H. CMR: DQPM =DQPN Cho D ABC có  = 300, B = 400 .Trên nmp bờ AB không chứa điểm C lấy điểm D sao cho BC = BD, ABÂC = ABÂD. CMR: AB là đường trung trực của CD. Gọi M là trung điểm AD. Đường thẳng vuông góc với AD tại M cắt AB tại N. CMR: NA = NC và tính góc DNÂB Cho 2 đoạn thẳng AB và CD cắt nhau tại trung điểm O của mỗi đoạn thẳng. CMR: AC =DB và AC // DB; AD =CB và AD // CB Vẽ CH ^ AB.Trên tia đối của tia OH lấy điểm I sao cho OI =OH.CMR: DI ^ AB Cho D ABC ( AB=AC). AD là phân giác. CMR : AD là đường trung trực. Vẽ BE ^ AC,BE cắt AD tại I. Trên tia AB lấy F sao cho AF = AE. CMR: IF ^ AB CMR : C, I, F thẳng hàng. Cho DABC có AB = AC. Lấy các điểm D, E theo thứ tự thuộc AB, AC sao cho AD = AE. Gọi O là giao điểm của BE và CD. CMR : DABM = DCAN và DBMC = DCNB Lấy E, F sao cho M là trugn điểm BE, N là trung điểm CF> CMR : A là trung điểm EF. CMR : MN // BC // EF Cho DABC, AH ^ BC, HI ^ AB, HK ^ AC. Lấy E, F sao cho I là trung điểm của HE, K là trung điểm của HF. EF cắt AB, AC lần lượt tại M, N. CMR : MH = ME và chu vi DMHN bằng EF CMR: AE = AF Biết BÂC = 600. Tính các góc DAEF 212. Cho vuông tại A. Trên BC lấy điểm D sao cho BD = DA. a. CMR: cân. So sánh và . b. Tia phân giác của cắt AC tại M. CMR: . c. CMR: MDBC. d. Đường thẳng qua A và song song với MB cắt đường thẳng BC tại E. CMR: B là trung điểm của DE. Cho góc bẹt xOy có tia phân giác Ot.Trên tia Ot lấy 2 điểm A, B( A nằm giữa O, B). Lấy C Ỵ Ox sao cho OC = OB, D Ỵ Oy sao cho OD = OA a. CMR: AC = BD và AC ^ BD b. Gọi M, N lần lượt là trung điểm của AC, BD. CMR: OM =ON c. Tính các góc của DMON d. CMR : AD ^ BC Cho DABC có  < 900. Trên cùng 1 nmp bờ AB không chứa C vẽ Ax ^ AB, Ay ^ AC. Trên Ax lấy D sao cho AD =AB và trên tia Ay lấy E sao cho AE = AC. a. CMR : BC = DE b. Gọi M, N lần lượt là trung điểm của BC, DE. Tính các góc của DMAN. Cho DABC.Trên tia đối của tia AB lấy điểm D sao cho AB = AD, trên tia đối của tia AC lấy E sao cho A là trung điểm CE. CMR: DE // BC M, N lần lượt là trung điểm của BC, DE. CMR : A là trung điểm MN CMR: AM // DE và AM = 2BE Gọi D là trung điểm BE.Các đường thẳng IA & CD cắt nhau ở K. CMR: IK // BC // DE và K là trung điểm DC Cho A, B, C, D sao cho AB // CD, AD // BC CMR: AB = CD, AD = BC Gọi O là giao điểm của AC, BD. CMR : O là trung điểm của mỗi đoạn AC, BD Cho DABC vuông tại A có AB=AC. Qua A kẻ đường thẳng xy ( B, C nằm cùng phía đối với xy) Vẽ BD ^ xy, CE ^ xy. CMR: DADB = DCEA DE = DB + EC Cho DABC ( AB=AC), D Ỵ AB, E Ỵ AC sao cho AD = AE. CMR : BE = CD Gọi O là giao điểm của BE và CD. CMR: DBOD = DCOE Gọi H là trung điểm của BC. CMR: A, O, H thẳng hàng. Cho góc xOy có Ot là phân giác. Qua điểm H Ỵ tia Ot kẻ đường vuông góc với tia Ot cắt Ox, Oy tai A, B. CMR : OA = OB Lấy C Ỵ OH. CMR : CA = CB AC cắt Oy tại D. Lấy E Ỵ Ox sao cho OE = OD. CMR: B, C, E thẳng hàng. Cho DABC ( B = C ) CMR : AB = AC BD là phân giác. Trên tia BA lấy E sao cho BE = CD. CMR : CE là phân giác CÂ. Gọi O là giao điểm của BD, CE. CMR: tia phân giác của  đi qua O
Tài liệu đính kèm:
 on tap toan 7(1).doc
on tap toan 7(1).doc





