Đề kiểm tra HK II môn: Toán 7

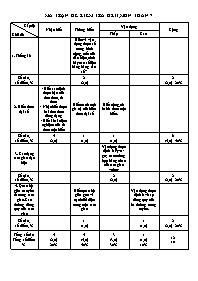
MA TRẬN ĐỀ KIỂM TRA HKII, MÔN TOÁN 7
 Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Cộng
Thấp
Cao
1. Thống kê
Hiểu và vận dụng được số trung bình cộng, mốt của dấu hiệu, trình bày các số liệu bằng bảng ‘‘tần số’’
Số câu, 
số điểm, %
2
(2,0)
2
(2,0) 20%
2. Biểu thức đại số
- Biết xác định được bậc của đơn thức, đa thức
- Nhận biết được hai đơn thức đồng dạng
- Biết khái niệm nghiệm của đa thức một biến 
Hiểu cách tính giá trị của biểu thức đại số
Biết cộng, trừ hai đa thức một biến.
Số câu, 
số điểm, %
4
(2,0)
1
(1,0)
1
(1,0)
6
(4,0) 40%
3. Các dạng tam giác đặc biệt
Vận dụng được định lí Py-ta-go; các trường hợp bằng nhau của tam giác vuông
Số câu, 
số điểm, %
2
(2,0)
2
(2,0) 20%
4. Quan hệ giữa các yếu tố trong tam giác. Các đường đồng quy của tam giác
Hiểu quan hệ giữa góc và cạnh đối diện trong một tam giác
Vận dụng được định lí về sự đồng quy của ba đường trung tuyến.
Số câu, 
số điểm, %
1
(1,0)
1
(1,0)
2
(2,0) 20%
Tổng số câu
Tổng số điểm
%
4
(2,0)
20%
4
(4,0)
40%
3
(3,0)
30%
1
(1,0)
10%
12
10
ĐỀ KIỂM TRA HKII (Năm học 2010 – 2011)
Môn: Toán 7
Thời gian: 90 phút (Không kể phát đề)
Câu 1: (2đ)
a) Xác định bậc của đơn thức: -2x3y5z
b) Xác định bậc của đa thức: 3x4y2+4x5-3xy+y5
c) Tìm hai đơn thức đồng dạng trong các đơn thức sau: 6x3y; xy3; -2x3; 5x3y; -2y3
d) Kiểm tra xem x = - 1 có là nghiệm của đa thức x2+4x+3 không?
Câu 2: (2đ) Cho hai đa thức: Px=5x4+2x3-3x2-2x+12 và Qx=-3x4+2x2+2x-32
a) Tính P(x) + Q(x) và P(x) – Q(x)
b) Tính giá trị của P(x) và Q(x) tại x = -1
Câu 3: (2đ) Một xạ thủ bắn súng có số điểm đạt được sau mỗi lần bắn được ghi lại trong bảng sau:
8 9 10 9 9 10 8 7 9 9
10 7 10 9 8 10 8 9 8 8
10 7 9 9 9 8 7 10 9 9
a) Lập bảng ‘‘tần số’’ và tìm mốt của dấu hiệu.
b) Tính số trung bình cộng của dấu hiệu (làm tròn đến chữ số thập phân thứ nhất).
Câu 4: (3đ) Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm; đường phân giác BE. 
 Kẻ EH vuông góc với BC (H ϵ BC). 
a) Chứng minh AB = BH.
b)Tính HC.
c) Chứng minh AE<EC
Câu 5: (1đ) Cho tam giác ABC, các đường trung tuyến BD và CE. Chứng minh rằng: BD+CE>32BC
ĐÁP ÁN VÀ THANG ĐIỂM
Câu 1: a) Bậc 9	(0,5đ)
 b) Bậc 6	(0,5đ)
 c) 6x3y và 5x3y	(0,5đ)
 d) x = -1 là nghiệm.	(0,5đ)
Câu 2: a) P(x) +Q(x) = 2x4+2x3-x2-1	(0,5đ)
 P(x) – Q(x) = 8x4+2x3-5x2-4x+2	(0,5đ)
 b) P(-1) = 52	(0,5đ)
 Q(-1) = -92	(0,5đ)
Câu 3: a) Bảng ‘‘tần số’’ 	(0,5đ)
Giá trị (x)
7 8 9 10
Tần số (n)
4 7 12 7
N=30
Mốt của dấu hiệu: M0=9	(0,5đ)
 b) Số trung bình cộng: X=7.4+8.7+9.12+10.730~8,7	(1,0đ)
Câu 4: 
	 a) Chứng minh được: ∆ABE = ∆HBE (Cạnh huyền – góc nhọn)	(0,75đ)
 	 => AB = BH	(0,25đ)
 b) AB = BH = 6 cm (Chứng minh trên)	(0,25đ)
 BC = 10 cm ( Theo định lí Py – ta – go )	(0,5đ)
 HC = BC – BH = 4 cm	(0,25đ)
 c) AE = EH (Do ∆ABE = ∆HBE)	(0,25đ)
 EH < EC (Do quan hệ giữa cạnh và góc đối diện)	(0,5đ)
 => AE < EC	(0,25đ)
Câu 5: - Gọi G là trọng tâm của ∆ABC.	
 - Trong ∆GBC có: BG + CG > BC (1)	(0,25đ)
 Ta có: BG = 23 BD , CG = 23 CE (Tính chất 3 đường trung tuyến)	(0,25đ)
 (1) => 23 BD + 23 CE > BC	(0,25đ)
 => 23 (BD +CE) > BC
 => BD + CE > 32 BC 	(0,25đ)