Đề thi olimpic năm 2010 môn: Toán 7

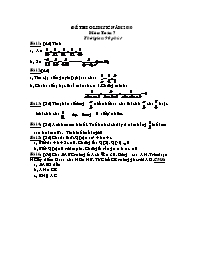
Đề thi Olimpic năm 2010
Môn: Toán 7
Thời gian: 90 phút
Bài 1: (4đ) Tính
a, A = 
b, S = 
Bài 2:(4đ) 
a, Tìm cặp số nguyên (a;b) sao cho: 
b, Cho ba số a; b; c thoả mãn abc = 1. Chứng minh:
Bài 3: (2đ) Tìm phân số dương nhỏ nhất sao cho lhi chia cho hoặc khi chia cho được thương là số tự nhiên.
Bài 4: (2đ) Anh hơn em 8 tuổi. Tuổi anh cách đây 5 năm bằng tuổi em sau 8 năm nữa. Tính tuổi mỗi người?
Bài 5: (2đ) Cho đa thức Q(x) = ax2 + bx + c
a, Biết 5a + b + 2c = 0. Chứng tỏ: Q(2) . Q(-1) 0
b, Biết Q(x) = 0 với mọi x. Chứng tỏ rằng: a = b = c = 0
Bài 6: (6đ) Cho ABC vuông ở A có = 300. Đường cao AH. Trên đoạn HC lấy điểm D sao cho HD = HB. Từ C kẻ CE vuông góc với AD. CMR:
a, ABD đều
b, AH = CE
c, EH // AC