Giáo án môn Hình học 7 năm 2005 - Tiết 59: Tính chất ba đường trung trực của tam giác

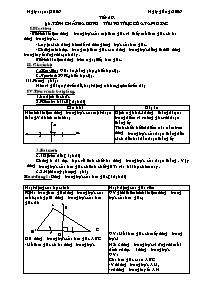
Ngày soạn: /2006 Ngày giảng: 2006
Tiết 59. 
Đ6. tính chất ba đường trung trực của tam giác
I.Mục tiêu:
-Biết khái niệm đường trung trực của một tam giác và thấy mỗi tam giác có ba đường trung trực. .
	- Luyện cách dùng ê ke để vẽ đườngtrung trực của tam giác.
	-Chứng minh được trong một tam giác can dường trung trực đồng thời là dường trung tuyến ứng với cạnh đáy.
	Biết khái niệm đường tròn ngoại tiếp tam giác.
II. Chuẩn bị:
1.Giáo viên: Giáo án, bảng phụ,phiếu học tập.
	2.Học sinh: SGK,phiếu học tập.
 III. Phương pháp:
	Nêu và giải quýet vấn đề, hoạt động nhóm, gợi mở vấn đáp
IV. Tiến trình bài giảng.
1 .ổn định tổ chức.
	2.Kiểm tra bài cũ ( 5 phút)
	Câu hỏi
Đáp án
Nêu khái niệm đường trung trực của một đoạn thẳng. Vẽ hình minh hoạ
Định nghĩa: Là dường thẳng đi qua trung điểm và vuông góc với đoạn thẳng ấy
Tính chất: bất kì điểm nào nằm tren đường trung trực của đoạn thẳng đều cách đều hai đầu đoạn thẳng ấy
3. Bài mới: 
3.1Đặt vấn đề: ( 1 phút)
Chúng ta đã được học về tính chất ba đường trung trực của đoạn thẳng . Vậy đường trung trực của tam giác có tính chất gì? Ta vào bài học hôm nay.
3.2.Nội dung- phươpng pháp
Hoạt động 1: 
Đường trung trực của tam giác( 15 phút)
Hoạt động của học sinh
Hoạt động của giáo viên
K/N: trong tam giácđường trung trực của mỗi cạnh gọi là đường trung trực của tam giác đó
D là đường trung trực của tam giác ABC
-Mỗi tam giác có ba đường trung trực
Nhận xét:
Tính chất: SGK/78
?1.
GT ABC, AB=AC, d VG với BC tại t 
 trung điểm M
KL A d( hay d là trung tuyến)
Chứng minh:
D là đường trung trực của BC, do dó d là tập hợp các cách đều B và C.
Mặt khác ABC cân AB=AC A thuộc d hay d là đường trung tuyến ứng với cạnh BC của tam giác ABC.
GV giới thiêuk khái niệm đường trung trực của tam giác;
GV: Mỗi tam giác có mấy đường trung trực?
HS: 3 đường trung trực vì ứng với mỗi đỉnh vẽ được 1 đường trung trực
GV:
Cho tam giác caan ABC
-Vẽ đường trung trực AM,
-vẽ đường trung tuyến AN
-Nhận xét về Hai đường trung tuyến và trung trực của tam giác cân trên từ đó rút ra tính chất
Học sinh hoạt động cá nhân trong 3 phút
Trình bày trong 2 phút
GV: hãy vẽ hình và chứng minh tính chất trên
Hoạt động 2: tính chất ba đường trung tuyến ( 13phút)
-Vẽ tam giác và dựng ba đường trung trực của tam giác đó
-Nhận xét về ba đường trung trực vừa dựng?
- Hãy phát biểu thành một định lí toán học?
Hoạt động của học sinh
Hoạt động của giáo viên
Định lí: SGK/78
0 là giao điểm ba dường trung trực của tam giác 0A=0B=0C
Chứng minh:
0 là trung trực của AB ta có 0A=0B ( 1)
: 0 là trung trực của BC ta có 0B=0C(2)
từ (1) và (2) 0A=0B=0C
chú ý: SGK/79
Hoạt động cá nhân trong 3 phút ghi 
 HS trình bày trong 2 phút
Giáo viên chốt lại định lí
GV: 0 là trung trực của AB ta có điều gì?
HS: 0A=0B
GV: 0 là trung trực của BC ta có điều gì?
HS: 0C=0B
Hs đọc chú ý
GV: để xác định tâm của đường trong ngoại tiếp tam giác ta làm như thé nào?
HS: Xác định giao điểm của ba đường trung trực
4 :Củng cố- luyện tập ( 8 phút)
Phát biểu các định lí về tính chất ba đường trung trực của tam giác
Bài tập 52
Hoạt động của học sinh
Hoạt động của giáo viên
Xét hai tam giácABH và ACH, có:
BH= CH
BHA= CHA
AH- cạnh chung
ABH = ACH ( c-g-c) AB= AC hay ABC cân
Để chứng minh ABC là tam giác cân ta cần chứng minh điều gì?
HS: B= C hoặc AB = AC
Để chứng minh B= C hoặc AB = AC ta làm như thế nào?
Hs: CM cho ABH= ACH
5: Hướng dẫn về nhà ( 2 phút)
-Học thuộc khái niệm đường trung trực của tam giác, định lí về tính chất ba đường trung trực của tam giác.
-Làm bài tập: 54,55,56,57.
-Chuẩn bị tiết sau luyện tập