Giáo án môn Hình học 7 năm 2006 - Tiết 49: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu

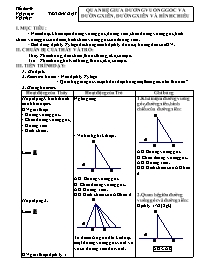
QUAN HỆ GIỮA ĐƯỜNG VUÔNG GÓC VÀ ĐƯỜNG XIÊN, ĐƯỜNG XIÊN VÀ HÌNH CHIẾU
Tiết thứ:49
Ngày soạn: TÊN BÀI DẠY
Ngày dạy:
I. MỤC TIÊU: 
	- Nắm được khái niệm đường vuông góc, đường xiên, chân đường vuông góc, hình chiếu vuông góc của điểm, hình chiếu vuông góc của đường xiên. 
	- Biết dùng định lý Pytago để chứng minh định lý dưới sự hướng dẫn của GV.
II. CHUẨN BỊ CỦA THẦY VÀ TRÒ:
	Thầy: Phim trong, đèn chiếu, thước thẳng, êke, compa.
	Trò: Phim trong, bút viết bảng, thước, eke, compa.
III. TIẾN TRÌNH DẠY:
Ổn định:
 2. Kiểm tra bài cũ:- Nêu định lý Pytago
	 - Quan hệ giữa góc và cạnh đối diện trong một tam giác như thế nào?
3. Giảng bài mới:
Hoạt động của Thầy
Hoạt động của Trò
Ghi bảng
Hoạt động1: hình thành các khái niệm.
GV giới thiệu:
- Đường vuông góc.
- Chân đường vuông góc, - Đường xiên
- Hình chiếu.
Làm ?1
Hoạt động 2: 
Làm ?2
GV giới thiệu định lý 1
- Để chứng minh trường hợp ngắn nhất dựa vào đâu?
Làm ?3
Làm ?4
a) Nếu HB > HC 
 AB > HC
b) Nếu AB > AC 
 HB > HC
c) Nếu HB = HC thì AB = AC và ngược lại 
AB = AC thì HB = HC 
Qua ?4, ta có định lý sau:
GV đưa định lý 2 lên màn hình.
Nghe giảng
- Vẽ hình, ghi kí hiệu.
AH: Đường vuông góc 	
H: Chân đường vuông góc.
AB: Đường xiên.
HB: Hình chiếu của AB trên d
Từ điểm A ngoài d ta kẻ được một đường vuông góc với d và vô số đường xiên đối với d.
Phát biểu định lý 1
- Dựa vào quan hệ giữa góc và cạnh đối diện trong tam giác.
Xét AHB vuông tại H ta có:
AB2 = AH2+HB2 do AB, AH, HB>0 nên AB > AH.
a) Nếu HB > HC thì AB>AC
Ta có: AB2 = AH2 + HB2 (1)
 AC2 = AH2 + HC2 (2)
Nếu HB > HC thì HB2 > HC2 
Suy ra AH2 +HB2 >AH2+HC2 
Do đó AB2 >AC2 vậy AB >AC
b) Nếu AB>AC thì AB2 >AC2 
Suy ra AH2 +HB2 >AH2+HC2 
Do đó HB2 >HC2 vậy HB >HC
c) AB = AC AH2 +HB2 = AH2+HC2 HB2 =HC2 HB =HC. 
HS phát biểu định lý 2.
1. Khái niệm đường vuông góc, đường xiên, hình chiếu của đường xiên:
AH: Đường vuông góc 	
H: Chân đường vuông góc.
AB: Đường xiên.
HB: Hình chiếu của AB trên d
2. Quan hệ giữa đường vuông góc và đường xiên:
Định lý 1/58 (Sgk)
 AH < AB 
Chứng minh (Sgk)
3. Các đường xiên và hình chiếu của chúng:
Định lý 2: (Sgk)
4:Củng cố: 
	+Phát biểu định lý 1 và định lý 2
	Bài 8/10(Sgk)
	c) HB < HC Đúng 
	(vì theo định lý 2 đường xiên nào lớn hơn thì có hình chiếu lớn hơn.)
A
B
C
D
M
5:Dặn dò:Bài 9, 10/59 (Sgk)
6. Hướng dẫn về nhà: Bài 9/59 
	So sánh MA với MB
 MB vóiMC 
 MC với MD 
	Kết luận MA – MB – MC – MD